Bolzano-Weierstrass selection principle
A method of proof which is frequently employed in mathematical analysis and which is based on successive subdivision of a segment into halves, after which the segment having some property is chosen as the new, initial segment. This method may be employed if the nature of the segments is such that the fact that the property is present in some segment implies that at least one segment obtained by halving the original segment will also have this property. For instance, if the segment contains infinitely-many points of some set, or if some function is not bounded on the segment, or if a non-zero function assumes values of opposite sign at the two ends of the segment — all these are properties of this type. The Bolzano–Weierstrass selection principle can be used to prove the Bolzano–Weierstrass theorem and a number of other theorems in analysis.
Depending on the criterion according to which the segments are chosen in applying the Bolzano–Weierstrass selection principle, the process obtained is effective or ineffective. An example of the former case is the application of the principle to prove that for a continuous real function that assumes values of opposite sign at the ends of a given segment, this segment contains a point at which the function vanishes (cf. Cauchy theorem on intermediate values of continuous functions). In this case the criterion chosen for the successive choice of the segments is that the function assumes values of different sign at the two ends of the chosen segment. If there is a way of computing the value of the function at every point, then, after performing a sufficient number of steps, it is possible to obtain the coordinates of the point at which the function vanishes, to within a given degree of accuracy. Thus, in addition to proving that a root of the equation 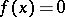 exists on a segment at the ends of which the values of the function are of different sign, one also has a method of approximately solving this equation. An example of an ineffective process is the use of the Bolzano–Weierstrass selection principle to prove that a continuous real function on a segment attains a maximum on the segment. Here, the segment chosen in the successive subdivisions is the one on which the maximum of the values of the function is not less than that on the other one. If, as in the former case, it is possible to calculate the value of the function at any point, this is still not sufficient for an effective choice of the required segment. Accordingly, the Bolzano–Weierstrass selection principle can be used in this case only to prove an existence theorem which says that the function assumes its maximum at some point, but not to specify this point within a given degree of accuracy.
exists on a segment at the ends of which the values of the function are of different sign, one also has a method of approximately solving this equation. An example of an ineffective process is the use of the Bolzano–Weierstrass selection principle to prove that a continuous real function on a segment attains a maximum on the segment. Here, the segment chosen in the successive subdivisions is the one on which the maximum of the values of the function is not less than that on the other one. If, as in the former case, it is possible to calculate the value of the function at any point, this is still not sufficient for an effective choice of the required segment. Accordingly, the Bolzano–Weierstrass selection principle can be used in this case only to prove an existence theorem which says that the function assumes its maximum at some point, but not to specify this point within a given degree of accuracy.
There exist various generalizations of the Bolzano–Weierstrass selection principle, e.g. to apply it in the  -dimensional Euclidean space (
-dimensional Euclidean space (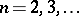 ) to
) to  -dimensional cubes, which are successively subdivided into congruent cubes with side-lengths of one-half that of the original cube.
-dimensional cubes, which are successively subdivided into congruent cubes with side-lengths of one-half that of the original cube.
Bolzano-Weierstrass selection principle. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Bolzano-Weierstrass_selection_principle&oldid=15469