Boks integral
One of the generalizations of the Lebesgue integral, proposed by A. Denjoy (1919) and studied in detail by T.J. Boks (1921). A real-valued function 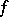 on a segment
on a segment 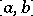 is periodically extended (with period length
is periodically extended (with period length 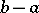 ) to the entire straight line. For an arbitrary subdivision
) to the entire straight line. For an arbitrary subdivision  of
of 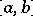 , for an arbitrary selection of points
, for an arbitrary selection of points 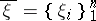 ,
, 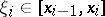 , and an arbitrary
, and an arbitrary 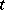 , the following sum is constructed:
, the following sum is constructed:
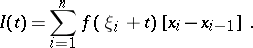 |
If, for 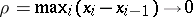 ,
, 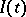 converges in measure to a definite limit
converges in measure to a definite limit 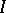 , the number
, the number 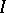 is said to be the Boks integral (
is said to be the Boks integral ( -integral) of
-integral) of 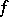 over
over  . Thus, the Boks integral is an integral of Riemann type and is a generalization of the Riemann integral.
. Thus, the Boks integral is an integral of Riemann type and is a generalization of the Riemann integral.
The Boks integral represents a considerable extension of the Lebesgue integral: Any summable function is 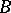 -integrable and these integrals coincide, but there exist non-summable
-integrable and these integrals coincide, but there exist non-summable 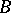 -integrable functions; in particular, if
-integrable functions; in particular, if 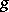 is the function conjugate with a summable function
is the function conjugate with a summable function 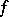 , then it is
, then it is 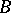 -integrable and the coefficients of the series conjugate with the Fourier series of
-integrable and the coefficients of the series conjugate with the Fourier series of 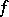 are the coefficients of the respective Fourier series (in the sense of
are the coefficients of the respective Fourier series (in the sense of 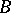 -integration) of
-integration) of 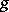 (A.N. Kolmogorov). The theory of the Boks integral was not further developed, since the
(A.N. Kolmogorov). The theory of the Boks integral was not further developed, since the 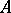 -integral proved to be more convenient for the integration of functions conjugate with summable functions.
-integral proved to be more convenient for the integration of functions conjugate with summable functions.
References
| [1] | T.J. Boks, "Sur les rapports entre les méthodes de l'intégration de Riemann et de Lebesque" Rend. Circ. Mat. Palermo (2) , 45 (1921) pp. 211–264 |
| [2] | A. Zygmund, "Trigonometric series" , 1–2 , Cambridge Univ. Press (1988) |
Boks integral. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Boks_integral&oldid=19058