Bohr compactification
The space  of maximal ideals of the algebra of Bohr almost-periodic functions (cf. Banach algebra; Bohr almost-periodic functions). The Bohr almost-periodic functions form a commutative
of maximal ideals of the algebra of Bohr almost-periodic functions (cf. Banach algebra; Bohr almost-periodic functions). The Bohr almost-periodic functions form a commutative  -algebra
-algebra  over the reals
over the reals  . The algebra
. The algebra  is isometrically isomorphic to the algebra
is isometrically isomorphic to the algebra  of all continuous functions on the compactum
of all continuous functions on the compactum  . The real line
. The real line  is naturally imbedded in
is naturally imbedded in  as an everywhere-dense subset (however, this imbedding is not a homeomorphism). The compactum
as an everywhere-dense subset (however, this imbedding is not a homeomorphism). The compactum 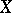 has the structure of a connected compact group which is identified with the group of characters of the real line if the latter is considered with the discrete topology. This isomorphism between the algebra of almost-periodic functions and the algebra of all continuous functions on the Bohr compactification makes it possible to simplify the proofs of a number of classical theorems. The concept of a Bohr compactification is also meaningful for the algebras of almost-periodic functions on other groups. In the case of the set of conditionally-periodic functions with
has the structure of a connected compact group which is identified with the group of characters of the real line if the latter is considered with the discrete topology. This isomorphism between the algebra of almost-periodic functions and the algebra of all continuous functions on the Bohr compactification makes it possible to simplify the proofs of a number of classical theorems. The concept of a Bohr compactification is also meaningful for the algebras of almost-periodic functions on other groups. In the case of the set of conditionally-periodic functions with  independent fixed periods, the
independent fixed periods, the  -dimensional torus with these periods acts as the Bohr compactification.
-dimensional torus with these periods acts as the Bohr compactification.
References
| [1] | L.H. Loomis, "An introduction to abstract harmonic analysis" , v. Nostrand (1953) |
Comments
Instead of Bohr compactification the term Bohr compactum is also used.
There are several other ways to characterize the Bohr compactification and to prove its existence; see e.g. [a1]. The most abstract one is the characterization of the Bohr compactification of a topological group 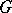 as the reflection of
as the reflection of 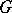 in the category of all compact Hausdorff topological groups; its existence is then guaranteed by the adjoint functor theorem. This approach is also used for semi-groups and leads to several other types of compactifications (e.g. the weakly almost-periodic compactifications). See [a2].
in the category of all compact Hausdorff topological groups; its existence is then guaranteed by the adjoint functor theorem. This approach is also used for semi-groups and leads to several other types of compactifications (e.g. the weakly almost-periodic compactifications). See [a2].
References
| [a1] | E.M. Alfsen, P. Holm, "A note on compact representations and almost periodicity in topological groups" Math. Scand. , 10 (1962) pp. 127–136 |
| [a2] | J.F. Berglund, H.D. Junghenn, P. Milnes, "Compact right topological semigroups and generalizations of almost periodicity" , Lect. notes in math. , 663 , Springer (1978) |
Bohr compactification. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Bohr_compactification&oldid=18252