Bohnenblust theorem
Consider the space $L ^ { p } ( \mu )$, $1 \leq p \leq \infty$, and a measure space $( \Omega , \mathcal A , \mu )$. Since the norm $\| \cdot \| p$ is $p$-additive, it is easily seen that the following condition is satisfied: For all $x , y , u , v \in L ^ { P } ( \mu )$ satisfying $\| x \| _ { p } = \| u \| _ { p }$, $\| y \| _ { p } = \| v \| _ { p }$, $x \perp y$ and $u \perp v$ (in the sense of disjoint support), one has $\| x + y \| _ { p } = \| u + v \| _ { p }$.
In [a2] H.F. Bohnenblust showed that the spaces $L ^ { p } ( \mu )$ are the only Banach lattices (cf. also Banach lattice) possessing this property; more precisely, he proved the following theorem, now known as the Bohnenblust theorem: Let $E$ be a Banach lattice of dimension $\geq 3$ satisfying $\| x + y \| = \| u + v \|$ for all $x , y , u , v \in E$ such that $\| x \| = \| u \|$, $\| y \| = \| v \|$, $x \perp y$, and $u \perp v$. Then there exists a $p$, $1 \leq p \leq \infty$, such that the norm on $E$ is $p$-additive.
Here, for $p < \infty$, a norm is said to be $p$-additive if $\| x \| ^ { p } + \| y \| ^ { p } = \| x + y \| ^ { p }$ for all $x , y \in E$ with $x \perp y$; a norm is said to be $\infty$-additive, or, equivalently, $E$ is said to be an $M$-space, if $\| x + y \| = \operatorname { max } \{ \| x \| , \| y \| \}$ for all $x , y \in E$ with $x \perp y$.
It should be noted that when $1 \leq p < \infty$, every Banach lattice with a $p$-additive norm is isometrically isomorphic to $L ^ { p } ( \mu )$, with $( \Omega , \mathcal A , \mu )$ a suitable measure space. This representation theorem is essentially due to S. Kakutani [a3], who considered the case $p = 1$; the proof of the more general result follows almost the same lines. For $p = \infty$ the situation is not so clear: there exist many $M$-spaces that are not isomorphic to any concrete $L ^ { \infty } ( \mu )$-space, for instance $c_0$.
In the proof of his theorem, H.F. Bohnenblust introduced an interesting and tricky method to construct the $p$ such that the norm is $p$-additive. A similar method was used later by M. Zippin [a5] to characterize $\mathbf{l}^{p}$-spaces in terms of bases. Since the proof given by Bohnenblust is interesting in itself, the main ideas are sketched below.
By hypothesis, there exists a function $F : [ 0 , \infty ) ^ { 2 } \rightarrow [ 0 , \infty )$ defined by
\begin{equation*} F ( s , t ) = \| t x + s y \| \text { for all } s , t \geq 0, \end{equation*}
whenever $x$ and $y$ are disjoint vectors of norm one. It can easily be verified that the function $F$ has the following properties:
1) $F ( 0 , t ) = t$;
ii) $F ( s , t ) = F ( t , s )$;
iii) $F ( r s , r t ) = r F ( s , t )$;
iv) $F ( r , F ( s , t ) ) = F ( F ( r , s ) , t )$;
v) $F ( s , t ) \leq F ( s _ { 1 } , t _ { 1 } )$ if $s\leq s_ 1$, $t \leq t_1$. The only non-trivial inclusion iv) follows from
\begin{equation*} F ( r , F ( s , t ) ) = \| r x + \| s y + t z \| z \| = \end{equation*}
\begin{equation*} = F ( s , t ) \left\| \frac { r } { F ( s , t ) } x + z \right\| = \end{equation*}
\begin{equation*} = F ( s , t ) \left\| \frac { r } { F ( s , t ) } x + \frac { 1 } { F ( s , t ) } ( s y + t z ) \right\| = \end{equation*}
\begin{equation*} = \| r x + s y + t z \| = F ( F ( r , s ) , t ) \end{equation*}
for all disjoint $x , y , z \in E _ { + }$ of norm one and $r , s , t \geq 0$ with $t \neq 0$.
One defines $a _ { 1 } = 1$ and $a _ { n + 1} = F ( 1 , a _ { n } )$ for all $n \geq 1$. Property v) implies that the sequence $( a _ { n } ) _ { n = 1 } ^ { \infty }$ is increasing. By induction one obtains $a _ { n + m} = F ( a _ { n } , a _ { m } )$ and 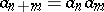 . If $a _ { 2 } = 1$, then properties i)–v) easily imply $F ( s , t ) = \operatorname { max } \{ s , t \}$ for all $s , t \geq 0$. Hence, $E$ is an $M$-space.
. If $a _ { 2 } = 1$, then properties i)–v) easily imply $F ( s , t ) = \operatorname { max } \{ s , t \}$ for all $s , t \geq 0$. Hence, $E$ is an $M$-space.
Assume now that $a _ { 2 } > 1$ and let $n \geq m \geq 2$. For all $i \in \mathbf{N}$ there exists a $k = k ( i ) \in \mathbf{N}$ such that $k \operatorname { log } m \leq i \operatorname { log } n < ( k + 1 ) \operatorname { log } m$. Since $( a _ { j } ) _ { j = 1 } ^ { \infty } $ is an increasing sequence, one concludes from $a _ { n^i } = ( a _ { n } )^i$ that $( a _ { m } ) ^ { k } \leq ( a _ { n } ) ^ { i } \leq ( a _ { m } ) ^ { k + 1 }$ or, equivalently, that $k \operatorname { log } a _ { m } \leq i \operatorname { log } a _ { n } \leq ( k + 1 ) \operatorname { log } a _ { m }$. This yields
\begin{equation*} \frac { k } { k + 1 } \frac { \operatorname { log } a _ { \mathfrak { m } } } { \operatorname { log } m } \leq \frac { \operatorname { log } a _ { \mathfrak { n } } } { \operatorname { log } n } \leq \frac { k + 1 } { k } \frac { \operatorname { log } a _ { \mathfrak { m } } } { \operatorname { log } m }. \end{equation*}
Letting $ k \rightarrow \infty$,
\begin{equation*} \frac { 1 } { p } : = \frac { \operatorname { log } a _ { m }} { \operatorname { log } m } = \frac { \operatorname { log } a _ { n } } { \operatorname { log } n }\; \text { for all } m , n \geq 2. \end{equation*}
It is clear that $p$ does not depend on the special choice of $m \in \mathbf{N}$. Moreover, $a _ { m } = m ^ { 1 / p }$ for all $m \in \mathbf{N}$. Since $a _ { n + m} = F ( a _ { n } , a _ { m } )$, it follows that $F ( m ^ { 1 / p } , n ^ { 1 / p } ) = ( n + m ) ^ { 1 / p }$ for all $n \in \mathbf N$. Consequently,
\begin{equation*} F ( s , t ) = ( s ^ { p } + t ^ { p } ) ^ { 1 / p }. \end{equation*}
From $F ( t , 1 - t ) = \| t x + ( 1 - t ) y \| \leq 1$ for all $0 \leq t \leq 1$ it follows that $p \geq 1$. This completes the proof.
Bohnenblust's theorem has some interesting consequences. For instance, T. Ando [a1] used it to prove that a Banach lattice $E$ is isometrically isomorphic to $L ^ { p } ( \mu )$ for some measure space $( \Omega , \mathcal A , \mu )$, or to some $c_0 ( \Gamma )$, if and only if every closed sublattice of $E$ is the range of a positive contractive projection.
References
| [a1] | T. Ando, "Banachverbände und positive Projektionen" Math. Z. , 109 (1969) pp. 121–130 |
| [a2] | H.F. Bohnenblust, "An axiomatic characterization of $L _ { p }$-spaces" Duke Math. J. , 6 (1940) pp. 627–640 |
| [a3] | S. Kakutani, "Concrete representation of abstract $L _ { p }$-spaces and the mean ergodic theorem" Ann. of Math. , 42 (1941) pp. 523–537 |
| [a4] | P. Meyer-Nieberg, "Banach lattices" , Springer (1991) |
| [a5] | M. Zippin, "On perfectly homogeneous bases in Banach spaces" Israel J. Math. , 4 A (1966) pp. 265–272 |
Bohnenblust theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Bohnenblust_theorem&oldid=55332