Bogolyubov theorem
Bogolyubov's edge-of-the-wedge theorem is a generalization of the principle of analytic continuation, in particular to the case of several complex variables. It was obtained in 1956 by N.N. Bogolyubov in the justification of the dispersion relations in quantum field theory ([1], Appendix A). The modern formulation is as follows. Let a function 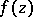 ,
, 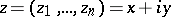 , be holomorphic in an open set
, be holomorphic in an open set 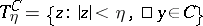 , where
, where 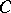 is an open cone in
is an open cone in 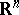 with apex at zero such that
with apex at zero such that 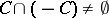 , let the open set
, let the open set 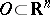 be contained in the ball
be contained in the ball 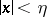 and suppose that for any test function
and suppose that for any test function 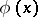 from
from 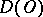 the limit
the limit
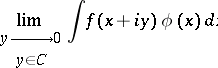 |
exists, independent from the way in which 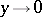 ,
, 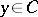 ; then
; then 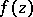 can be analytically continued into the domain
can be analytically continued into the domain  :
:
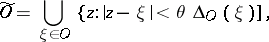 |
where 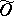 is a complex neighbourhood of the set
is a complex neighbourhood of the set 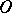 ,
, 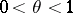 is a constant which depends only on the cone
is a constant which depends only on the cone 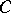 , and
, and 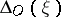 is the distance from the point
is the distance from the point 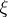 to the boundary of
to the boundary of 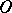 . Bogolyubov's edge-of-the-wedge theorem also remains valid if
. Bogolyubov's edge-of-the-wedge theorem also remains valid if 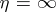 . In such a case, and under certain assumptions regarding the growth of the function
. In such a case, and under certain assumptions regarding the growth of the function 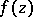 , one obtains the original formulation of Bogolyubov (cf. [1]; the light cone in
, one obtains the original formulation of Bogolyubov (cf. [1]; the light cone in 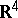 plays the role of the cone). There exist various proofs and generalizations of this theorem [2], [5]. In particular, one can mention the generalizations to hyperfunctions [4] and to holomorphic cocycles [3].
plays the role of the cone). There exist various proofs and generalizations of this theorem [2], [5]. In particular, one can mention the generalizations to hyperfunctions [4] and to holomorphic cocycles [3].
Bogolyubov's edge-of-the-wedge theorem is extensively employed in axiomatic quantum field theory, in the theory of partial differential equations and in the theory of boundary values of holomorphic functions (especially of functions of several complex variables). A useful completion of the theorem is the 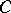 -convex hull theorem [2]. Let, under the conditions of Bogolyubov's theorem,
-convex hull theorem [2]. Let, under the conditions of Bogolyubov's theorem, 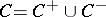 ,
, 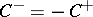 , where
, where 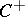 is a convex sharp cone; then
is a convex sharp cone; then
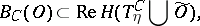 |
where 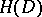 is the envelope of holomorphy (cf. Holomorphic envelope) of
is the envelope of holomorphy (cf. Holomorphic envelope) of 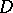 ,
, 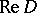 is the real section of the domain
is the real section of the domain 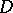 , and
, and  is the
is the 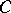 -convex hull of the set
-convex hull of the set 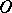 , i.e. the smallest open set containing
, i.e. the smallest open set containing 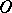 and having the following property: If the points
and having the following property: If the points 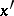 and
and 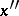 of
of 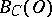 can be connected by a
can be connected by a 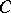 -similar curve that is totally contained in
-similar curve that is totally contained in 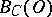 , then all
, then all 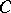 -similar curves homotopic to it are located in
-similar curves homotopic to it are located in 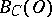 .
.
References
| [1] | N.N. Bogolyubov, D.V. Shirkov, "Introduction to the theory of quantized fields" , Interscience (1959) (Translated from Russian) |
| [2] | V.S. Vladimirov, "Methods of the theory of functions of several complex variables" , M.I.T. (1966) (Translated from Russian) |
| [3] | A. Martineau, "Distributions et valeurs au bord des fonctions holomorphes" , Theory of distributions. Proc. internat. summer inst. , Lisbon (1964) pp. 193–326 |
| [4] | H. Komatsu (ed.) , Hyperfunctions and pseudodifferential equations. Proc. Conf. Katata, 1971 , Lect. notes in math. , 287 , Springer (1973) |
| [5] | W. Rudin, "Lectures on the edge-of-the-wedge theorem" , Amer. Math. Soc. (1971) |
Comments
Additional generalizations of the edge-of-the-wedge theorem include the case where 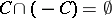 , see [5], and the case where the "edge" of the "wedge" is a totally-real hypersurface in
, see [5], and the case where the "edge" of the "wedge" is a totally-real hypersurface in 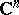 instead of an open set in
instead of an open set in 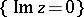 in
in 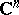 , see [a1]. For cones
, see [a1]. For cones 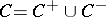 , where
, where 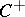 is convex, a
is convex, a 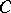 -similar curve in
-similar curve in 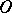 is defined as a differentiable curve
is defined as a differentiable curve 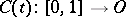 such that
such that 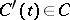 .
.
References
| [a1] | E. Bedford, "Holomorphic continuation at a totally real edge" Math. Ann. , 230 (1977) pp. 213–225 |
Bogolyubov's theorem on singularities of type 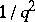 . A theorem in statistical mechanics on the asymptotic behaviour of Green functions (cf. Green function) in the limit of small momenta (
. A theorem in statistical mechanics on the asymptotic behaviour of Green functions (cf. Green function) in the limit of small momenta (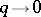 ) for Bose and Fermi systems with a gauge-invariant interaction potential. Presented in 1961 by N.N. Bogolyubov [1].
) for Bose and Fermi systems with a gauge-invariant interaction potential. Presented in 1961 by N.N. Bogolyubov [1].
The following inequality is valid for systems of several interacting particles in the case of a degenerate statistical equilibrium state for the two-time temperature commutator Green functions (cf. Green function in statistical mechanics) in the energy representation:
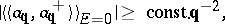 | (1) |
where 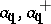 are the annihilation and creation operators of a particle with momentum
are the annihilation and creation operators of a particle with momentum 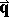 .
.
The singularities in the Green functions specified in Bogolyubov's theorem which appear when 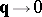 correspond to elementary excitations in the physical system under study. Bogolyubov's theorem also predicts the asymptotic behaviour for small momenta of macroscopic properties of the system which are connected with Green functions by familiar theorems.
correspond to elementary excitations in the physical system under study. Bogolyubov's theorem also predicts the asymptotic behaviour for small momenta of macroscopic properties of the system which are connected with Green functions by familiar theorems.
Thus, according to (1), in the case of superfluid Bose or Fermi systems, the particle density distribution  tends to infinity as
tends to infinity as 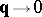 at a rate which is not slower than
at a rate which is not slower than 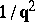 . In such a case the degeneracy of the state of statistical equilibrium is due to the conservation law of the total number of particles, i.e. to the invariance of the Hamiltonian of the system with respect to gauge transformations. However, similar singularities appear in the respective Green functions, and hence also in the correlation functions characterizing systems with other kinds of degeneracy caused by certain additional conservation laws, i.e. by the invariance of the Hamiltonian of the system with respect to certain transformations. Bogolyubov's theorem has a number of non-trivial physical consequences, involving problems of long-range ordering in systems of many interacting particles in which a spontaneous symmetry breaking manifests itself in various ways: the Heisenberg model with ferromagnetic, anti-ferromagnetic and ferrimagnetic ordering, systems of superfluid and superconducting types and systems with crystalline ordering.
. In such a case the degeneracy of the state of statistical equilibrium is due to the conservation law of the total number of particles, i.e. to the invariance of the Hamiltonian of the system with respect to gauge transformations. However, similar singularities appear in the respective Green functions, and hence also in the correlation functions characterizing systems with other kinds of degeneracy caused by certain additional conservation laws, i.e. by the invariance of the Hamiltonian of the system with respect to certain transformations. Bogolyubov's theorem has a number of non-trivial physical consequences, involving problems of long-range ordering in systems of many interacting particles in which a spontaneous symmetry breaking manifests itself in various ways: the Heisenberg model with ferromagnetic, anti-ferromagnetic and ferrimagnetic ordering, systems of superfluid and superconducting types and systems with crystalline ordering.
The appearance of singularities in the Green functions as 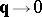 is connected with the presence of a branch of collective excitations in the energy spectrum of the system that corresponds with spontaneous symmetry breaking under certain restrictions on the interaction potential.
is connected with the presence of a branch of collective excitations in the energy spectrum of the system that corresponds with spontaneous symmetry breaking under certain restrictions on the interaction potential.
The nature of the energy spectrum of elementary excitations may be studied with the aid of the mass operator inequality constructed for Green functions of type (1). In the case of Bose systems, for a finite temperature 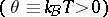 , this inequality has the form:
, this inequality has the form:
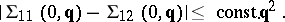 | (2) |
If  , formula (2) yields a generalization of the so-called Hugenholtz–Pines formula to finite temperatures. If one assumes that the mass operator is regular in a neighbourhood of the point
, formula (2) yields a generalization of the so-called Hugenholtz–Pines formula to finite temperatures. If one assumes that the mass operator is regular in a neighbourhood of the point 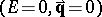 , then one can use (2) to prove the absence of a gap in the (phonon-type) excitation energy spectrum.
, then one can use (2) to prove the absence of a gap in the (phonon-type) excitation energy spectrum.
In the case of zero temperatures (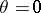 ) inequality (1) establishes a connection between the density of the continuous distribution of the particle momenta and the minimum energy of an excited state.
) inequality (1) establishes a connection between the density of the continuous distribution of the particle momenta and the minimum energy of an excited state.
Relations of type (1) should also be valid in quantum field theory, in which a spontaneous symmetry breaking (at a transition between two ground states) results [4], [5] in an infinite number of particles of zero mass (Goldstone's theorem), which are interpreted as singularities for small momenta in the quantum field Green functions. Bogolyubov's theorem has been applied to a relativistic quantum-field model with a spontaneous symmetry breaking [6].
References
| [1] | N.N. Bogolyubov, , Selected works , 3 , Kiev (1970) (In Russian) |
| [2] | B.I. Sadovnikov, V.K. Fedyanin, "N.N. Bogoljubov's inequalities in systems of many interacting particles with broken symmetry" Teoret. Mat. Fiz. , 16 : 3 (1973) pp. 368–393 (In Russian) (English abstract) |
| [3] | N.N. Bogolyubov jr., B.I. Sadovnikov, "Some questions in statistical mechanics" , Moscow (1975) (In Russian) |
| [4] | J. Goldstone, "Field theories with "superconductor" solutions" Nuovo Cimento (10) , 19 (1961) pp. 154–164 (Italian abstract) |
| [5] | J. Goldstone, A. Salam, S. Weinberg, "Broken symmetries" Phys. Rev. (2) , 127 (1962) pp. 965–970 |
| [6] | A.K. Kazanskii, Teoret. Mat. Fiz. , 22 : 3 (1975) pp. 418–421 |
A.M. Kurbatov
Bogolyubov theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Bogolyubov_theorem&oldid=16527