Blumberg theorem
In 1922, H. Blumberg [a1] proved that if 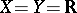 , the real number set, then:
, the real number set, then:
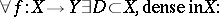 | (a1) |
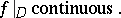 |
Even for functions 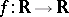 , the set
, the set 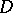 in (a1) cannot be made to have cardinality
in (a1) cannot be made to have cardinality  (see [a2]). S. Baldwin (see the references of [a6]) showed that it is consistent with the axioms of set theory that the set
(see [a2]). S. Baldwin (see the references of [a6]) showed that it is consistent with the axioms of set theory that the set 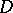 in (a1) can always be chosen to be uncountably dense; the set
in (a1) can always be chosen to be uncountably dense; the set 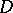 cannot be necessarily chosen so that, for one-to-one functions,
cannot be necessarily chosen so that, for one-to-one functions, 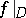 is a homeomorphism (C. Goffman; see the references of [a6]); further, the set
is a homeomorphism (C. Goffman; see the references of [a6]); further, the set 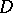 cannot necessarily be chosen so as to make
cannot necessarily be chosen so as to make 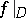 differentiable or monotonic (see J. Cedar; see the references of [a6]). Despite the above, J.B. Brown (see the references of [a6]) proved that for every
differentiable or monotonic (see J. Cedar; see the references of [a6]). Despite the above, J.B. Brown (see the references of [a6]) proved that for every 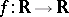 there exists a set
there exists a set 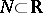 ,
, 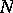 being
being  -dense in
-dense in 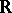 , such that
, such that 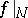 is pointwise discontinuous (relative to
is pointwise discontinuous (relative to 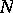 ).
).
Blumberg spaces.
Let 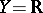 . A space
. A space  is called a Blumberg space if (a1) holds for
is called a Blumberg space if (a1) holds for 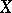 . J.C. Bradford and Goffman [a3] proved that a metric space
. J.C. Bradford and Goffman [a3] proved that a metric space 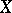 is Blumberg if and only if
is Blumberg if and only if 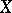 is a Baire space, i.e., a space in which open, non-empty subsets are of the second category. The key lemma in their proof is the Banach category theorem. H.E. White [a4] extended the Bradford–Goffman theorem to topological spaces
is a Baire space, i.e., a space in which open, non-empty subsets are of the second category. The key lemma in their proof is the Banach category theorem. H.E. White [a4] extended the Bradford–Goffman theorem to topological spaces 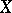 which have
which have 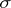 -disjoint pseudo-bases (cf. also Topological space). He also showed that the real number set
-disjoint pseudo-bases (cf. also Topological space). He also showed that the real number set 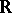 with the density topology is a Baire space which is not Blumberg. W.A.R. Weiss (see the references of [a5]) gave an example of a compact Hausdorff space which is not Blumberg. Z. Piotrowski and A. Szymański [a7] showed that if
with the density topology is a Baire space which is not Blumberg. W.A.R. Weiss (see the references of [a5]) gave an example of a compact Hausdorff space which is not Blumberg. Z. Piotrowski and A. Szymański [a7] showed that if 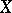 is a space for which (a1) holds with
is a space for which (a1) holds with 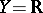 , then (a1) holds for every second-countable space
, then (a1) holds for every second-countable space 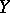 . The following characterization is of interest (see [a7]): A space is Blumberg if and only if for every countable covering
. The following characterization is of interest (see [a7]): A space is Blumberg if and only if for every countable covering 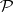 of
of 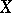 there exists a dense subset
there exists a dense subset  of
of 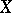 such that
such that 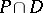 is open in
is open in 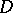 for every
for every 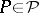 , see also [a8] for more characterizations. General references for this area are [a5], [a6].
, see also [a8] for more characterizations. General references for this area are [a5], [a6].
The simple example of the identity function from the real number set with the Euclidean topology into the real number set with the discrete topology exhibits the necessity of certain restrictions placed upon the range space. Spaces 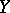 for which (a1) holds, where
for which (a1) holds, where 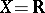 , were studied in [a9].
, were studied in [a9].
The dynamics of Blumberg spaces.
It is easy to see that a dense or closed subspace of a Blumberg space need not be Blumberg. The Stone–Čech compactification of a dense subspace of a completely regular Blumberg space is a Blumberg space, a result of R. Levy and R.H. McDowell (see the references of [a7]).
The Cartesian product of Blumberg spaces need not be a Blumberg space, since there is a metric Baire space (hence Blumberg space) whose square is not Baire. On the other hand, S. Todorčević [a10] showed that there is a first-countable compact space 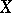 that is not Blumberg, whereas
that is not Blumberg, whereas 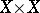 is a Blumberg space. It follows from the above theorem that the image of a Blumberg space under an open and continuous function need not be Blumberg.
is a Blumberg space. It follows from the above theorem that the image of a Blumberg space under an open and continuous function need not be Blumberg.
Consider the union 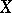 of the graph
of the graph 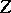 of the function
of the function 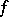 defined by
defined by 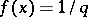 if
if 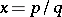 in lowest terms,
in lowest terms, 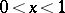 , and a copy
, and a copy 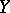 of the rational number set between
of the rational number set between  and
and 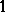 . The natural projection of
. The natural projection of 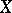 onto
onto 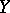 (which is constant on
(which is constant on 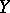 ) shows that even perfect, continuous functions do not necessarily preserve Blumberg spaces. In contrast, Blumberg spaces are preserved in pre-images under irreducible surjections [a7].
) shows that even perfect, continuous functions do not necessarily preserve Blumberg spaces. In contrast, Blumberg spaces are preserved in pre-images under irreducible surjections [a7].
M. Valdivia [a11] showed that (a1) holds for linear transformations, where 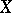 and
and 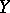 are metrizable linear spaces and
are metrizable linear spaces and 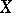 is of the second category. L. Drewnowski subsequently proved that "dense subset" in Valdivia's theorem cannot be replaced by "dense linear subspace" .
is of the second category. L. Drewnowski subsequently proved that "dense subset" in Valdivia's theorem cannot be replaced by "dense linear subspace" .
Blumberg sets, i.e. dense sets 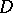 appearing in (a1), have been studied in connection with characterizations of certain almost-continuous functions, such as quasi-continuous functions ([a13]).
appearing in (a1), have been studied in connection with characterizations of certain almost-continuous functions, such as quasi-continuous functions ([a13]).
References
| [a1] | H. Blumberg, "New properties of all real functions" Trans. Amer. Math. Soc. , 3 (1922) pp. 113–128 |
| [a2] | W. Sierpiński, A. Zygmund, "Sur une fonction que est discontinue sur tout ensemble de puissance de continue" Fundam. Math. , 4 (1923) pp. 316–318 |
| [a3] | J.C. Bradford, C. Goffman, "Metric spaces in which Blumberg's theorem holds" Proc. Amer. Math. Soc. , 11 (1960) pp. 667–670 |
| [a4] | H.E. White, Jr., "Topological spaces in which Blumberg's theorem holds" Proc. Amer. Math. Soc. , 44 (1974) pp. 454–462 |
| [a5] | J.B. Brown, "Variations on Blumberg's theorem" Real Anal. Exchange , 9 (1983/84) pp. 123–137 |
| [a6] | J.B. Brown, "Restriction theorems in real analysis" Real Anal. Exchange , 20 (1994/5) pp. 510–526 |
| [a7] | Z. Piotrowski, A. Szymanski, "Concerning Blumberg's theorem" Houston J. Math. , 10 (1984) pp. 109–115 |
| [a8] | A. Szymański, "On  -Baire and -Baire and 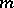 -Blumberg spaces" , Proc. Conf. Topology and Measure II (Rostock–Warnemunde, GDR, 1977) , Part I , Greifswald (1980) pp. 151–161 -Blumberg spaces" , Proc. Conf. Topology and Measure II (Rostock–Warnemunde, GDR, 1977) , Part I , Greifswald (1980) pp. 151–161 |
| [a9] | J.B. Brown, Z. Piotrowski, "Co-Blumberg spaces" Proc. Amer. Math. Soc. , 96 (1986) pp. 686–688 |
| [a10] | S. Todorčević, "Stationary sets, trees and continuums" Publ. Inst. Math. , 27 (1981) pp. 249–262 |
| [a11] | M. Valdivia, "On the closed graph theorem in topological spaces" Manuscr. Math. , 23 (1978) pp. 173–184 |
| [a12] | M. Wilhelm, "Nearly lower semicontinuity and its applications" , General Topology and its Applications (Fifth Prague Topology Symp.) , Heldermann (1981) pp. 692–698 |
| [a13] | T. Nebrunn, "Quasi-continuity" Real Anal. Exchange , 14 (1988–89) pp. 259–306 |
Blumberg theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Blumberg_theorem&oldid=18487