Bloch wave
A generic term used to name a family of (special) functions which provide the spectral resolution of elliptic differential operators with periodic coefficients. In the mathematics literature, the study of differential equations with periodic coefficients is known as Floquet theory [a12] (cf. also Linear system of differential equations with periodic coefficients; Floquet theory). In physics, it goes under the name Bloch waves method because it was F. Bloch [a5] who first introduced this technique in his study of the motion of an electron in a crystalline solid. Since crystals have a periodic structure, this amounts to studying propagation of waves in such media and more exactly, to the spectral analysis of the Schrödinger equation with a periodic potential. In time, this method has been very well-developed and applied to various situations.
In light of the examples discussed below, it will be seen that Bloch waves are periodic functions in a generalized sense, and more precisely, they are families of functions which depend on a vector parameter, say $\eta \in \mathbf{R} ^ { N }$, that have the form
\begin{equation*} \psi ( y ) = e ^ { i \eta . y } \phi ( y ) \text { a.e. for } y \in \mathbf{R} ^ { N }, \end{equation*}
where $\phi$ is a non-zero $[ 0,2 \pi [ ^ { N } $-periodic function (in the classical sense). Alternatively, Bloch waves can be seen as functions that satisfy a generalized periodicity condition of the following kind: for all $p \in \mathbf{Z} ^ { N }$,
\begin{equation} \tag{a1} \psi ( y + 2 \pi p ) = e ^ { 2 \pi i \eta \cdot p } \psi ( y )\, \text { for a.e. } \ y \in \mathbf{R} ^ { N }. \end{equation}
Functions enjoying this property are called $( \eta , Y )$-periodic, where $Y = [ 0,2 \pi [ ^ { N } $. The space $Y$ is referred to as the reference cell. It is clear from (a1) that if $ \eta $ is replaced by $\eta + q$ with $q \in \mathbf{Z} ^ { N }$, then this generalized periodicity condition remains unaltered and $ \eta $ can therefore be confined to the cell $Y ^ { \prime } = [ 0,1 [ ^ { N }$. The cell $Y ^ { \prime }$ is referred to as the reciprocal cell of $Y$. (In the physics literature, $Y ^ { \prime }$ is known as the first Brillouin zone).
Examples.
Consider the spectral analysis of the Laplace operator $- \Delta$ in $\mathbf{R} ^ { N }$. Of course, this is a very simple case where it is not yet necessary to work with Bloch waves, as it corresponds to an operator with constant coefficients, but it is very instructive to motivate the above class of generalized periodic functions. As usual, $- \Delta$ is considered as an unbounded operator acting in $L ^ { 2 } ( R ^ { N } )$ and with domain $D ( - \Delta ) = H ^ { 2 } ( \mathbf{R} ^ { N } )$. It is well known that the spectrum of this operator consists of the non-negative real axis and that the plane waves $e ^ { i \eta . y}$ with $| \eta | ^ { 2 } = \lambda$ can be considered as "generalized eigenfunctions" with "eigenvalue" $\lambda > 0$ (cf. also Spectral analysis). These functions are not elements of $L ^ { 2 } ( R ^ { N } )$ but they span all of $L ^ { 2 } ( R ^ { N } )$, since they provide the spectral resolution of the identity in the sense of Fourier inversion:
\begin{equation*} f ( y ) = \frac { 1 } { ( 2 \pi ) ^ { N / 2 } } \int _ { \mathbf{R} ^ { N } } \widehat { f } ( \eta ) e ^ { i \eta . y } d \eta . \end{equation*}
From a physical viewpoint, in this example it is implicitly assumed that $\mathbf{R} ^ { N }$ is filled by a homogeneous medium since $- \Delta$ has constant coefficients. In such situations, it is customary that the spectral resolution of the corresponding operator be obtained by Fourier analysis and plane waves. These latter functions obviously satisfy (a1). Thus, in passing from the constant-coefficient case to that of periodic ones, it seems natural to impose (a1). Bloch waves can therefore be thought of as coming out of the interaction between plane waves and a periodic medium.
In the case quoted above, the medium does not vary at all. At the other extreme lie media that oscillate, i.e., media which can be represented by non-constant periodic coefficients. It is precisely in the spectral analysis of such operators that the so-called Bloch waves arise naturally, playing the role of generalized eigenfunctions. In order to illustrate this, consider one of the most representative examples in this field, namely the operator
\begin{equation*} {\cal A} = - \sum _ { k , \operatorname{l} = 1 } ^ { N } \frac { \partial } { \partial y _ { k } } ( a _ { k \operatorname{l} } ( y ) \frac { \partial } { \partial y_{\operatorname{l}} } ), \end{equation*}
where the coefficients $a _ { k \text{l} }$ are assumed to be smooth, symmetric, $Y$-periodic, and satisfy the ellipticity condition: there exists an $\alpha > 0$ such that for all $y , \xi \in {\bf R }^ { N }$, $a _ { k \text{l} } ( y ) \xi _ { k } \xi _ { \text{l} } \geq \alpha | \xi | ^ { 2 }$. The Bloch waves method to obtain the spectral resolution of $\mathcal{A}$ in $L ^ { 2 } ( R ^ { N } )$ consists of introducing a family of spectral problems parametrized by $\eta \in Y ^ { \prime }$: Find $\lambda = \lambda ( \eta )$ and $\psi = \psi ( y ; \eta ) \not\equiv 0$ such that
\begin{equation*} \mathcal{A} \psi (. ; \eta ) = \lambda \psi (. ; \eta ) \text{ in }\mathbf{R} ^ { N }, \end{equation*}
\begin{equation*} \psi ( . ; \eta ) \text { is } ( \eta , Y) \square \text{periodic}. \end{equation*}
Solutions $\psi$ of this family of (generalized periodic) spectral problems are called Bloch waves or Bloch eigenvectors. Following the scheme for Bloch waves suggested above, one looks for solutions $\psi$ that are products of $Y$-periodic functions with solutions in the homogenized media (i.e., plane waves): $\psi ( y ; \eta ) = e ^ { i \eta .y } \phi ( y ; \eta )$, where $\phi ( \, . \, ; \eta )$ is $Y$-periodic. This transformation maps the spectral problem for $\psi$ into a new problem, where the parameter $ \eta $ appears in the operator rather than in the boundary condition: Find $\lambda = \lambda ( \eta )$ and $\phi = \phi ( y ; \eta )$ (not identically zero) such that
\begin{equation*} \mathcal{A} ( \eta ) \phi = \lambda \phi\, \text { in } \mathbf{R} ^ { N }, \end{equation*}
\begin{equation*} \phi ( . , \eta ) Y \square \text{ periodic}. \end{equation*}
Here, the operator $\mathcal{A} ( \eta )$ is defined by
\begin{equation*} \mathcal{A} ( \eta ) = - \sum _ { k , \operatorname {l} = 1 } ^ { N } \left( \frac { \partial } { \partial y _ { k } } + i \eta _ { k } \right) \left( a _ { k \operatorname {l} } ( y ) \left( \frac { \partial } { \partial y _ { \operatorname {l} } } + i \eta _ { \operatorname {l} } \right) \right), \end{equation*}
and it is referred to as the shifted operator.
For each fixed $\eta \in Y ^ { \prime }$, the above spectral problems admit a discrete sequence of eigenvalues with the following properties:
$0 \leq \lambda _ { 1 } ( \eta ) \leq \ldots \leq \lambda _ { m } ( \eta ) \leq \ldots \rightarrow \infty$,
each $\lambda _ { m } ( \eta )$ defines a Lipschitz continuous function of $ \eta $ in $Y ^ { \prime }$. Besides, the corresponding eigenfunctions, denoted by $\{ \psi _ { m } ( . ; \eta ) \} _ { m = 1 } ^ { \infty } $ and $\{ \phi _ { m } ( . ; \eta ) \} _ { m = 1 } ^ { \infty } $, form orthonormal bases of the spaces of all $L _ { \text{loc}} ^ { 2 } ( R ^ { N } )$-functions that are $( \eta , Y )$-periodic or $Y$-periodic, respectively.
Thanks to the above parametrized family of eigenvalues and eigenfunctions, one can completely describe the spectral resolution of $\mathcal{A}$ as an unbounded self-adjoint operator in $L ^ { 2 } ( R ^ { N } )$. Roughly speaking, the results are as follows: On one hand, the spectrum of $\mathcal{A}$, denoted by $\sigma ( A )$, has a band structure and, more exactly, it coincides with the so-called Bloch spectrum, which is defined as
\begin{equation*} \sigma ( \mathcal A ) = \sigma _ { \operatorname{Bloch} } = \bigcup _ { m = 1 } ^ { \infty } \left[ \operatorname { min } _ { \eta \in Y ^ { \prime } } \lambda _ { m } ( \eta ) , \operatorname { max } _ { \eta \in Y ^ { \prime } } \lambda _ { m } ( \eta ) \right]. \end{equation*}
On the other hand, the family $\{ e ^ { i \eta . y } \phi _ { m } ( y ; \eta ) \}$, $m \geq 1$, $\eta \in Y ^ { \prime }$, forms a basis of $L ^ { 2 } ( R ^ { N } )$ in a generalized sense, and $L ^ { 2 } ( R ^ { N } )$ can be identified with $L ^ { 2 } ( Y ^ { \prime } , \text{l} ^ { 2 } ( \mathbf{N} ) )$ via the Parseval equality. More precisely, let $g \in L ^ { 2 } ( {\bf R} ^ { N } )$ be an arbitrary given function. For every $m \geq 1$, let the $m$th Bloch coefficient of $g$ be defined as:
\begin{equation*} \hat{g} _ { m } ( \eta ) = \int _ { \mathbf{R} ^ { N } } g ( y ) e ^ { - i \eta . y} \overline { \phi } m ( y ; \eta ) d y , \forall \eta \in Y ^ { \prime }. \end{equation*}
Then the following inverse formula holds:
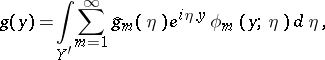 |
and furthermore, Parseval's identity holds:
\begin{equation*} \int _ { \mathbf{R} ^ { N } } | g ( y ) | ^ { 2 } d y = \int _ { Y ^ { \prime } } \sum _ { m = 1 } ^ { \infty } | \hat{g} _ { m } ( \eta ) | ^ { 2 } d \eta. \end{equation*}
History.
As already mentioned at the beginning, Bloch waves were first introduced in solid state physics in the spectral analysis of the Schrödinger operator with a periodic potential, i.e., the operator $S = - \Delta + W$, where $W$ is a periodic function. (Notice that $\mathcal{S}$ represents an intermediate situation between $\mathcal{A}$ and $- \Delta$.) As a result, the existing extensive physics literature on this subject concentrates essentially on this case; see [a6], [a10], [a15], Vol. IV, [a20]. By contrast, the mathematical theory has developed much more slowly. The first result is due to I.M. Gel'fand [a13]. In his paper, he outlines a proof of a Parseval-type identity for functions in $L ^ { 2 } ( R ^ { N } )$; variations were developed by E.C. Titchmarsh [a18], V.B. Lidskii, and M. Eastham [a11]. A more complete discussion of Bloch waves was published by F. Odeh and J.B. Keller [a14]. The interesting question concerning the measurability of Bloch waves with respect to $ \eta $ was studied by C. Wilcox [a19]. Overall views of these topics can be found in [a7], [a16].
Without taking away merit from the historical importance that the Bloch waves method has had in spectral theory, it is important to mention that, more recently (1990s), Bloch waves have been applied successfully in other branches of mathematics, notably in homogenization theory. (For an excellent introduction to this subject, see [a4]). The pioneering work of A. Bensoussan, J.L. Lions and G. Papanicolaou [a4] permitted one to envisage that Bloch waves could also be used in the homogenization of elliptic operators with periodically oscillating coefficients. Their ideas led recently (1990s) to the introduction and development of the so-called Bloch waves homogenization method, different versions of which appeared in [a1], [a4], [a8], [a17], and whose mathematical justification is due to C. Conca and M. Vanninathan [a9]. This method has made it possible to deal with numerous mathematical, physical and engineering problems which were out of reach using traditional techniques. Examples can be found in the field of fluid-solid interactions, or that of periodic homogenization, where this method has brought about new insights and has offered an alternative way to view the classical approaches (see [a2], [a7], [a8], [a9]), and also in the analysis of boundary layers in homogenization, where it has provided a new understanding of the asymptotic behaviour of the spectrum of periodic structures (see [a3]).
References
| [a1] | F. Aguirre, C. Conca, "Eigenfrequencies of a tube bundle immersed in a fluid" Appl. Math. Optim. , 18 (1988) pp. 1–38 |
| [a2] | G. Allaire, C. Conca, "Bloch-wave homogenization for a spectral problem in fluid-solid structures" Arch. Rat. Mech. Anal. , 135 (1996) pp. 197–257 |
| [a3] | G. Allaire, C. Conca, "Boundary layers in the homogenization of a spectral problem in fluid-solid structures" SIAM J. Math. Anal. , 29 (1998) pp. 343–379 |
| [a4] | A. Bensoussan, J.L. Lions, G. Papanicolaou, "Asymptotic analysis in periodic structures" , North-Holland (1978) |
| [a5] | F. Bloch, "Über die Quantenmechanik der Electronen im Kristallgitern" Z. Phys. , 52 (1928) pp. 555–600 |
| [a6] | L. Brillouin, "Propagation of waves in periodic structures" , Dover (1953) |
| [a7] | C. Conca, J. Planchard, M. Vanninathan, "Fluids and periodic structures" , Wiley&Masson (1995) |
| [a8] | C. Conca, M. Vanninathan, "A spectral problem arising in fluid-solid structures" Comput. Meth. Appl. Mech. Eng. , 69 (1988) pp. 215–242 |
| [a9] | C. Conca, M. Vanninathan, "Homogenization of periodic structures via Bloch decomposition" SIAM J. Appl. Math. , 57 (1997) pp. 1639–1659 |
| [a10] | A.P. Cracknell, K.C. Wong, "The Fermi surface" , Clarendon Press (1973) |
| [a11] | M. Eastham, "The spectral theory of periodic differential equations" , Scottish Acad. Press (1973) |
| [a12] | G. Floquet, "Sur les équations différentielles linéaires à coefficients périodiques" Ann. Ecole Norm. Ser. 2 , 12 (1883) pp. 47–89 |
| [a13] | I.M. Gelfand, "Entwicklung nach Eigenfunktionen einer Gleichung mit periodischer Koeffizienten" Dokl. Akad. Nauk SSSR , 73 (1950) pp. 1117–1120 |
| [a14] | F. Odeh, J.B. Keller, "Partial differential equations with periodic coefficients and Bloch waves in crystals" J. Math. Phys. , 5 (1964) pp. 1499–1504 |
| [a15] | M. Reed, B. Simon, "Methods of modern mathematical physics" , Acad. Press (1978) |
| [a16] | J. Sánchez–Hubert, E. Sánchez–Palencia, "Vibration and coupling of continuous systems" , Springer (1989) |
| [a17] | F. Santosa, W.W. Symes, "A dispersive effective medium for wave propagation in periodic composites" SIAM J. Appl. Math. , 51 (1991) pp. 984–1005 |
| [a18] | E.C. Titchmarsh, "Eigenfunctions expansions Part II" , Clarendon Press (1958) |
| [a19] | C. Wilcox, "Theory of Bloch waves" J. Anal. Math. , 33 (1978) pp. 146–167 |
| [a20] | J.M. Ziman, "Principles of the theory of solids" , Cambridge Univ. Press (1972) |
Bloch wave. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Bloch_wave&oldid=50749