Blaschke factor
Let  be the open unit disc in the complex plane
be the open unit disc in the complex plane  . A holomorphic function
. A holomorphic function
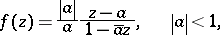 |
on  is called a Blaschke factor if it occurs in a Blaschke product
is called a Blaschke factor if it occurs in a Blaschke product
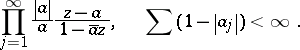 |
The defining properties of a Blaschke factor are:
a) a Blaschke factor has precisely one zero in  ;
;
b) a Blaschke factor has norm  on the boundary of
on the boundary of  .
.
The properties a)–b) may be used to define Blaschke factors on a Dirichlet domain  in a Riemann surface as
in a Riemann surface as  . Here,
. Here,  is the Green function for
is the Green function for  at
at 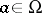 and
and  is its (multiple-valued) harmonic conjugate. See [a1] for the planar case.
is its (multiple-valued) harmonic conjugate. See [a1] for the planar case.
Thus, in general a Blaschke factor will not be single valued, but it is single valued on simply-connected domains.
Next, for functions 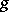 of the Nevanlinna class (cf. Boundary properties of analytic functions), the term "Blaschke factor" is used to indicate the Blaschke product that has the same zeros as
of the Nevanlinna class (cf. Boundary properties of analytic functions), the term "Blaschke factor" is used to indicate the Blaschke product that has the same zeros as 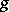 . For example, on the disc
. For example, on the disc  one has the decomposition formula
one has the decomposition formula
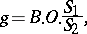 |
where 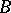 is a Blaschke product or the Blaschke factor,
is a Blaschke product or the Blaschke factor, 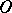 is the outer factor, and
is the outer factor, and 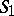 ,
,  are singular inner functions; cf. [a2], Boundary properties of analytic functions; Hardy classes.
are singular inner functions; cf. [a2], Boundary properties of analytic functions; Hardy classes.
Similar decomposition theorems are known for domains in Riemann surfaces, cf. [a3].
References
| [a1] | S.D. Fischer, "Function thory on planar domains" , Wiley (1983) |
| [a2] | J.B. Garnett, "Bounded analytic functions" , Acad. Press (1981) |
| [a3] | M. Voichick, L. Zalcman, "Inner and outer functions on Riemann Surfaces" Proc. Amer. Math. Soc. , 16 (1965) pp. 1200–1204 |
Blaschke factor. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Blaschke_factor&oldid=17194