Bivector
A class  of ordered pairs
of ordered pairs  of vectors of an affine space
of vectors of an affine space  , starting at a common origin (considered in a basis of the underlying space). A bivector is considered to be equal to zero if its constituent vectors
, starting at a common origin (considered in a basis of the underlying space). A bivector is considered to be equal to zero if its constituent vectors  and
and  are collinear. A non-zero bivector generates a unique two-dimensional space in
are collinear. A non-zero bivector generates a unique two-dimensional space in  , its carrier. Two bivectors are said to be parallel if their carrier planes are parallel. If
, its carrier. Two bivectors are said to be parallel if their carrier planes are parallel. If  has finite dimension
has finite dimension  , and
, and  are the contravariant coordinates of
are the contravariant coordinates of  , while
, while 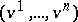 are the contravariant coordinates of
are the contravariant coordinates of  , calculated with respect to some basis
, calculated with respect to some basis 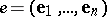 of the underlying space of
of the underlying space of 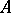 , then the quantities
, then the quantities
 |
are called the Plücker coordinates of the pair 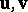 . Two pairs of vectors are in the same class if their Plücker coordinates with respect to some basis coincide (they will then be equal in any basis). The coordinates of the class are then called the coordinates of the bivector
. Two pairs of vectors are in the same class if their Plücker coordinates with respect to some basis coincide (they will then be equal in any basis). The coordinates of the class are then called the coordinates of the bivector 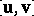 with respect to the basis
with respect to the basis  . These coordinates are skew-symmetric with respect to their indices; they contain
. These coordinates are skew-symmetric with respect to their indices; they contain 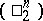 independent coordinates. Under a transition to another basis of
independent coordinates. Under a transition to another basis of 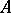 , the coordinates of a bivector behave as coordinates of a twice-contravariant tensor. A bivector is also called a free bivector. In the presence of a scalar product in
, the coordinates of a bivector behave as coordinates of a twice-contravariant tensor. A bivector is also called a free bivector. In the presence of a scalar product in 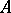 , a number of metrical concepts of vector algebra can be extended to bivectors. The measure of a bivector is the area of the parallelogram formed by the vectors
, a number of metrical concepts of vector algebra can be extended to bivectors. The measure of a bivector is the area of the parallelogram formed by the vectors 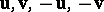 , the origin of each one being located in the end of the preceding one. This only depends on the class, not on the representatives
, the origin of each one being located in the end of the preceding one. This only depends on the class, not on the representatives 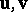 . The scalar product of two bivectors is the number equal to the product of the measures of the factors by the cosine of the angle between their two carrier planes. This product is a bilinear form of the coordinates of the factors, the coefficients of which are defined by the metric tensor of the space
. The scalar product of two bivectors is the number equal to the product of the measures of the factors by the cosine of the angle between their two carrier planes. This product is a bilinear form of the coordinates of the factors, the coefficients of which are defined by the metric tensor of the space 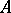 alone.
alone.
If the dimension of 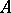 is 3, the bivector
is 3, the bivector 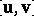 may be identified with a vector of
may be identified with a vector of 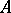 which, in the presence of a scalar product, is called the vector product of the vectors
which, in the presence of a scalar product, is called the vector product of the vectors  .
.
In tensor calculus a bivector is an arbitrary contravariant skew-symmetric tensor of valency 2 (i.e. a tensor of type 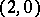 ). Each such tensor may be represented as a sum of tensors, to which correspond non-zero bivectors in the above sense with different carrier planes. They define the sheets of the bivector. The rank of the skew-symmetric matrix of dimension
). Each such tensor may be represented as a sum of tensors, to which correspond non-zero bivectors in the above sense with different carrier planes. They define the sheets of the bivector. The rank of the skew-symmetric matrix of dimension 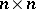 consisting of the coordinates of a bivector is an even number
consisting of the coordinates of a bivector is an even number 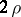 , where
, where 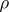 is the number of sheets of the bivector. In a real affine space
is the number of sheets of the bivector. In a real affine space 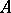 this matrix is similar to the matrix
this matrix is similar to the matrix
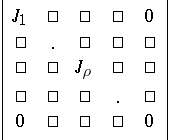 |
with the blocks
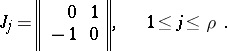 |
See also Exterior product; Poly-vector; Plücker coordinates.
References
| [1] | J.A. Schouten, "Tensor analysis for physicists" , Cambridge Univ. Press (1951) |
Comments
Assign to a non-zero bivector  the plane it generates, i.e. the corresponding point of the Grassmannian of 2 planes in (the underlying vector space of)
the plane it generates, i.e. the corresponding point of the Grassmannian of 2 planes in (the underlying vector space of)  . Then the Plücker coordinates of this element in the Grassmann manifold can be identified with the Plücker coordinates of the bivector.
. Then the Plücker coordinates of this element in the Grassmann manifold can be identified with the Plücker coordinates of the bivector.
References
| [a1] | E. Cartan, "Geometry of Riemannian spaces. (With notes and appendices by R. Hermann)" , Math. Sci. Press (1983) (Translated from French) |
| [a2] | S. Gołab, "Tensor calculus" , Elsevier (Translated from Polish) |
| [a3] | P.K. [P.K. Rashevskii] Rashewski, "Riemannsche Geometrie und Tensoranalyse" , Deutsch. Verlag Wissenschaft. (1959) (Translated from Russian) |
Bivector. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Bivector&oldid=18904