Birth-and-death process
A Markov process with states  in which in a time interval
in which in a time interval  transitions from the state
transitions from the state  into the states
into the states  and
and  occur with probabilities
occur with probabilities  and
and  , respectively, and where the probability of other transitions is
, respectively, and where the probability of other transitions is  . For a special choice of the reproduction coefficients
. For a special choice of the reproduction coefficients  and the death coefficients
and the death coefficients 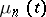 one can obtain particular cases which provide a satisfactory description of various real processes: radioactive transformations, the running of telephone exchanges, the evolution of biological populations, etc. The fact that birth-and-death processes are widely used in applications is due to the simplicity of the equations for the transition probabilities, which often can be obtained explicitly. For instance, in the case of a Poisson process
one can obtain particular cases which provide a satisfactory description of various real processes: radioactive transformations, the running of telephone exchanges, the evolution of biological populations, etc. The fact that birth-and-death processes are widely used in applications is due to the simplicity of the equations for the transition probabilities, which often can be obtained explicitly. For instance, in the case of a Poisson process 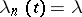 ,
, 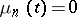 , the probabilities
, the probabilities 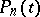 (
(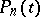 is the probability of being at time
is the probability of being at time  in the state
in the state  if the process has started from state
if the process has started from state  ) satisfy the system:
) satisfy the system:
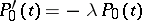 |
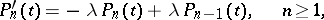 |
where
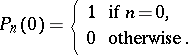 |
The solution of this system is:
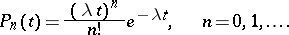 |
A more general process is the one in which 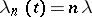 ,
,  . This type of process was first studied by G. Yule (1924) in connection with the mathematical theory of evolution. A Yule process is a particular case of a pure birth process which is obtained from the general birth-and-death process by assuming
. This type of process was first studied by G. Yule (1924) in connection with the mathematical theory of evolution. A Yule process is a particular case of a pure birth process which is obtained from the general birth-and-death process by assuming 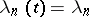 ,
, 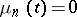 . If
. If 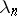 increases very rapidly, then with positive probability one can pass through all states in a finite time and then
increases very rapidly, then with positive probability one can pass through all states in a finite time and then
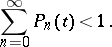 |
The condition
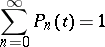 |
for a pure birth process is satisfied if and only if the series 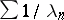 diverges. If
diverges. If 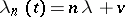 ,
, 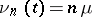 , then the birth-and-death process is a branching process with immigration in which the state
, then the birth-and-death process is a branching process with immigration in which the state  designates the number of particles. Each particle dies during time
designates the number of particles. Each particle dies during time 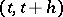 with probability
with probability 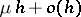 , splits into two particles with probability
, splits into two particles with probability 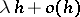 and, moreover, one particle immigrates from the outside with probability
and, moreover, one particle immigrates from the outside with probability 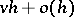 . If
. If 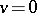 then one obtains the simplest branching process without immigration. If
then one obtains the simplest branching process without immigration. If 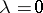 and
and 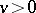 , then this type of process with immigration can be applied to describe the functioning of a telephone exchange with an infinite number of lines. Here, the state is the number of occupied lines. The reproduction coefficient
, then this type of process with immigration can be applied to describe the functioning of a telephone exchange with an infinite number of lines. Here, the state is the number of occupied lines. The reproduction coefficient 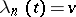 characterizes the rate of incoming telephone calls, and
characterizes the rate of incoming telephone calls, and  is the expected duration of a conversation.
is the expected duration of a conversation.
References
| [1] | W. Feller, "An introduction to probability theory and its applications" , 1–2 , Wiley (1957–1971) |
| [2] | B.A. [B.A. Sevast'yanov] Sewastjanow, "Verzweigungsprozesse" , Akad. Wissenschaft. DDR (1974) (Translated from Russian) |
| [3] | R.L. Saaty, "Elements of queueing theory with applications" , McGraw-Hill (1961) |
Comments
References
| [a1] | K.B. Athreya, P.E. Ney, "Branching processes" , Springer (1972) |
Birth-and-death process. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Birth-and-death_process&oldid=12092