Birkhoff normal form
Birkhoff–Gustavson normal form
Usually, a formal normal form (cf. Normal form of a system of differential equations) for a time-independent Hamiltonian system in the neighbourhood of a stationary point (cf. Normal form in a neighbourhood of a fixed point) for which the linearized system at the stationary point has only purely imaginary eigenvalues.
Consider a Hamiltonian system on 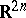 with Hamiltonian
with Hamiltonian 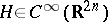 , i.e.
, i.e.
 |
with  ,
,  ,
, 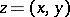 ,
,
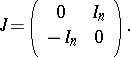 |
Suppose that 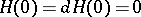 . The origin is a stationary point and the Hamiltonian evaluated at the origin is
. The origin is a stationary point and the Hamiltonian evaluated at the origin is
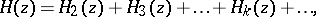 |
where 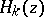 denotes the homogeneous terms of degree
denotes the homogeneous terms of degree 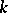 . Furthermore, suppose that the matrix of the linearized system,
. Furthermore, suppose that the matrix of the linearized system, 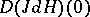 , is diagonalizable (over
, is diagonalizable (over 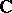 ) with purely imaginary eigenvalues
) with purely imaginary eigenvalues 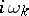 ,
, 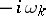 ,
,  . Let
. Let 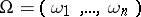 . The eigenvalues are called resonant if they are rationally dependent, i.e. if there is an integer-valued vector
. The eigenvalues are called resonant if they are rationally dependent, i.e. if there is an integer-valued vector  such that
such that 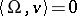 , where
, where  is the standard inner product on
is the standard inner product on  . The eigenvalues are non-resonant if there is no such relation.
. The eigenvalues are non-resonant if there is no such relation.
On 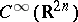 , define Poisson brackets by
, define Poisson brackets by 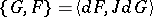 , where
, where 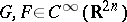 . Considering
. Considering 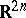 with the symplectic structure given by the standard symplectic form (see [a1]),
with the symplectic structure given by the standard symplectic form (see [a1]), 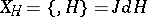 is the Hamiltonian vector field generated by
is the Hamiltonian vector field generated by 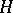 .
.
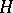 is said to be in normal form up to order
is said to be in normal form up to order 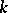 with respect to
with respect to 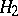 if
if 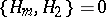 for
for 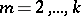 .
. 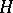 can be transformed into normal form using transformations of the type
can be transformed into normal form using transformations of the type 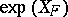 . These transformations can be considered as the time-
. These transformations can be considered as the time-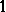 flow of the vector field
flow of the vector field 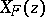 , and therefore as symplectic diffeomorphisms on
, and therefore as symplectic diffeomorphisms on 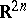 . They can also be considered as differential operators acting on the space of homogeneous polynomials of degree
. They can also be considered as differential operators acting on the space of homogeneous polynomials of degree 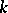 . These two points of view are related by the fact that
. These two points of view are related by the fact that  . Applying a transformation
. Applying a transformation 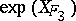 with generating function
with generating function 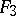 homogeneous of degree three gives
homogeneous of degree three gives
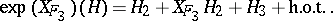 |
The terms of degree three are 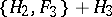 . Consequently all terms in
. Consequently all terms in 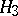 that are in the image of
that are in the image of 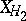 can be removed by making the appropriate choice for the generating function
can be removed by making the appropriate choice for the generating function 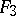 . After having made a choice for
. After having made a choice for 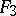 one gets
one gets
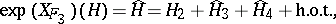 |
with 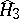 in some complement of
in some complement of 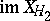 .
.
Next, consider a transformation 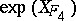 now taking a generating function
now taking a generating function 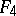 homogeneous of degree four. This gives
homogeneous of degree four. This gives
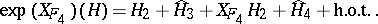 |
Thus, now one can remove all terms in 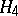 that are in the image of
that are in the image of 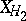 . Repeating this process means that up to arbitrary degree one can remove all terms of
. Repeating this process means that up to arbitrary degree one can remove all terms of 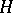 that are in the image of
that are in the image of 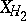 . This leads to the following idea of normal form:
. This leads to the following idea of normal form: 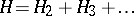 is in normal form up to degree
is in normal form up to degree 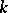 with respect to
with respect to 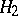 if
if  ,
, 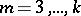 , are in some complement of
, are in some complement of 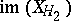 . When the linearized system is diagonalizable,
. When the linearized system is diagonalizable, 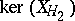 can be chosen as a complement to
can be chosen as a complement to 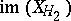 , giving
, giving 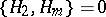 ,
, 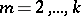 . Letting
. Letting  , one gets a formal normal form.
, one gets a formal normal form.
More on the basic ideas sketched above can be found in [a10], [a1], [a2]. The above idea was first used, although in an implicit way, by G.D. Birkhoff [a3] for deriving a normal form in the non-resonant case. Attention was again drawn to normal forms by F.G. Gustavson's paper [a7], where he obtained a formal normal form for the resonant cases. A similar normal form was obtained earlier by J. Moser [a9]. Gustavson emphasized that by normalizing up to infinite order extra formal integrals are obtained. The normal form has more symmetry than the original system.
The above ideas have been extended to the case where the linearized system has purely imaginary eigenvalues but is not diagonalizable [a8]. A normal form theory for non–Hamiltonian vector fields has also been developed along the above lines by using the Lie bracket of vector fields rather than Poisson brackets of functions [a4], [a6]. The most general context to formulate the theory is that of reductively filtered Lie algebras [a11].
Normal forms are of importance in the qualitative theory of differential equations. In particular, they play a role in bifurcation theory. Using Lyapunov–Schmidt reduction and the theory of singularities of differentiable mappings one can determine which number of terms of the normal form is sufficient to describe the bifurcation of stationary points and periodic solutions up to topological equivalence [a5], [a6], [a8].
References
| [a1] | R. Abraham, J.E. Marsden, "Foundations of mechanics" , Benjamin/Cummings (1978) |
| [a2] | V.I. Arnol'd, V.V. Kozlov, A.I. Neishstadt, "Mathematical aspects of classical and celestial mechanics" , Dynamical systems III , Springer (1988) (In Russian) |
| [a3] | G.D. Birkhoff, "Dynamical systems" , Amer. Math. Soc. Colloqium Publ. , IX , Amer. Math. Soc. (1927) |
| [a4] | R.H. Cushman, J.A. Sanders, "Nilpotent normal forms and representation theory of 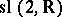 " M. Golubitsky (ed.) J. Guckenheimer (ed.) , Multiparameter Bifurcation Theory , Contemp. Math. , 56 , Amer. Math. Soc. (1986) pp. 31–51 " M. Golubitsky (ed.) J. Guckenheimer (ed.) , Multiparameter Bifurcation Theory , Contemp. Math. , 56 , Amer. Math. Soc. (1986) pp. 31–51 |
| [a5] | M. Golubitsky, D.G. Schaeffer, "Singularities and groups in bifurcation theory I" , Appl. Math. Sci. , 51 , Springer (1985) |
| [a6] | M. Golubitsky, I. Stewart, D.G. Schaeffer, "Singularities and groups in bifurcation theory II" , Appl. Math. Sci. , 69 , Springer (1988) |
| [a7] | F.G. Gustavson, "On constructing formal integrals of a Hamiltonian system near an equilibrium point" Astron. J. , 71 (1966) pp. 670–686 |
| [a8] | J.C. van der Meer, "The Hamiltonian Hopf bifurcation" , Lecture Notes in Mathematics , 1160 , Springer (1985) |
| [a9] | J. Moser, "New aspects in the theory of Hamiltonian systems" Comm. Pure Appl. Math. , 9 (1958) pp. 81–114 |
| [a10] | J. Moser, "Lectures on Hamiltonian systems" , Memoirs , 81 , Amer. Math. Soc. (1968) pp. 1–60 |
| [a11] | J.A. Sanders, "Versal normal form computations and representation theory" E. Tournier (ed.) , Computer Algebra and Differential Equations , London Math. Soc. Lecture Notes , 193 , Cambridge Univ. Press (1994) pp. 185–210 |
Birkhoff normal form. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Birkhoff_normal_form&oldid=17284