Birkhoff-Rott equation
A planar vortex sheet is a curve in a two-dimensional inviscid incompressible flow across which the tangential velocity is discontinuous (cf. also Von Kármán vortex shedding). The vortex sheet is described by its complex position  . For simplicity, assume that the vorticity on the sheet is all positive and that the flow outside the sheet is irrotational. The sheet is parameterized by a real variable
. For simplicity, assume that the vorticity on the sheet is all positive and that the flow outside the sheet is irrotational. The sheet is parameterized by a real variable  which represents the circulation, i.e.
which represents the circulation, i.e.  is the vorticity density along the sheet. Vortex sheet evolution is then described by the Birkhoff–Rott equation [a1], [a11]:
is the vorticity density along the sheet. Vortex sheet evolution is then described by the Birkhoff–Rott equation [a1], [a11]:
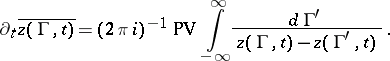 | (a1) |
Because of the singularity of the integral at  , the integral in (a1) is understood as a Cauchy principal value integral (cf. also Cauchy integral).
, the integral in (a1) is understood as a Cauchy principal value integral (cf. also Cauchy integral).
Perturbations of a flat sheet of uniform strength grow due to the linear Kelvin–Helmholtz instability and at some time later the sheet begins to roll-up. D. Moore [a8], [a9] showed by asymptotic analysis that a singularity could develop along the sheet at finite time starting from smooth initial data. The singularity found by Moore has the form  in which
in which  is the position and
is the position and  is the circulation variable. This singularity form was later found to be generic [a16]. Exact singular solutions of the non-linear Birkhoff–Rott equation, corresponding to Moore's singularity, have been constructed in [a3], [a4].
is the circulation variable. This singularity form was later found to be generic [a16]. Exact singular solutions of the non-linear Birkhoff–Rott equation, corresponding to Moore's singularity, have been constructed in [a3], [a4].
Numerical simulations of the vortex sheet problem [a5], [a7], [a12] have produced singular solutions which are in agreement with Moore's theory. Krasny's method [a5] used a non-linear filter to remove the numerical noise generated by the physical instability, the convergence of which was proved in [a15] for analytic initial data. R. Krasny [a6] also computed roll-up of a sheet, using a desingularized equation, and found that the sheet begins to roll-up immediately after the appearance of the first singularity. A general set of similarity solutions for a rolled-up vortex sheet were constructed numerically in [a10].
Existence results almost up to the singularity time have been proved [a2], [a13], using the abstract Cauchy–Kovalevskaya theorem. The results for existence and for singularity formation use an extension of the Birkhoff–Rott equation (a1) into the complex  -plane for analytic initial data. Since the linearization of (a1) is elliptic in
-plane for analytic initial data. Since the linearization of (a1) is elliptic in 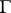 and
and 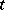 (cf. also Elliptic partial differential equation), it is hyperbolic in the imaginary
(cf. also Elliptic partial differential equation), it is hyperbolic in the imaginary 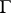 direction (cf. also Hyperbolic partial differential equation). Singularities in the initial data at complex values of
direction (cf. also Hyperbolic partial differential equation). Singularities in the initial data at complex values of 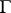 travel towards the real axis at a finite speed.
travel towards the real axis at a finite speed.
The Birkhoff–Rott equation has been extended to three-dimensional sheets in [a14]. Short-time existence theory for the three-dimensional equations has been established in [a13]. A computational method for the three-dimensional equations was implemented in [a17].
Open questions as of 2000 include the well-posedness for continuation after Moore's singularity and the form of singularities in three dimensions.
References
| [a1] | G. Birkhoff, "Helmholtz and Taylor instability" , Proc. Symp. Appl. Math. , XII , Amer. Math. Soc. (1962) pp. 55–76 |
| [a2] | R.E. Caflisch, O.F. Orellana, "Long time existence for a slightly perturbed vortex sheet" Commun. Pure Appl. Math. , 39 (1986) pp. 807–838 |
| [a3] | R.E. Caflisch, O.F. Orellana, "Singularity formulation and ill-posedness for vortex sheets" SIAM J. Math. Anal. , 20 (1989) pp. 293–307 |
| [a4] | J. Duchon, R. Robert, "Global vortex sheet solutions of Euler equations in the plane" J. Diff. Eqs. , 73 (1988) pp. 215–224 |
| [a5] | R. Krasny, "On singularity formation in a vortex sheet and the point vortex approximation" J. Fluid Mech. , 167 (1986) pp. 65–93 |
| [a6] | R. Krasny, "Desingularization of periodic vortex sheet roll-up" J. Comput. Phys. , 65 (1986) pp. 292–313 |
| [a7] | D.I. Meiron, G.R. Baker, S.A. Orszag, "Analytic structure of vortex sheet dynamics, Part 1, Kelvin–Helmholtz instability" J. Fluid Mech. , 114 (1982) pp. 283–298 |
| [a8] | D.W. Moore, "The spontaneous appearance of a singularity in the shape of an evolving vortex sheet" Proc. Royal Soc. London A , 365 (1979) pp. 105–119 |
| [a9] | D.W. Moore, "Numerical and analytical aspects of Helmholtz instability" F.I. Niordson (ed.) N. Olhoff (ed.) , Theoretical and Applied Mechanics (Proc. XVI ICTAM) , North-Holland (1984) pp. 629–633 |
| [a10] | D.I. Pullin, W.R.C. Phillips, "On a generalization of Kaden's problem" J. Fluid Mech. , 104 (1981) pp. 45–53 |
| [a11] | N. Rott, "Diffraction of a weak shock with vortex generation" JFM , 1 (1956) pp. 111 |
| [a12] | M. Shelley, "A study of singularity formation in vortex-sheet motion by a spectrally accurate vortex method" J. Fluid Mech. , 244 (1992) pp. 493–526 |
| [a13] | P. Sulem, C. Sulem, C. Bardos, U. Frisch, "Finite time analyticity for the two and three dimensional Kelvin–Helmoltz instability" Comm. Math. Phys. , 80 (1981) pp. 485–516 |
| [a14] | R.E. Caflisch, X. Li, "Lagrangian theory for 3D vortex sheets with axial or helical symmetry" Transport Th. Statist. Phys. , 21 (1992) pp. 559–578 |
| [a15] | R.E. Caflisch, T.Y. Hou, J. Lowengrub, "Almost optimal convergence of the point vortex method for vortex sheets using numerical filtering" Math. Comput. , 68 (1999) pp. 1465–1496 |
| [a16] | S.J. Cowley, G.R. Baker, S. Tanveer, "On the formation of Moore curvature singularities in vortex sheets" J. Fluid Mech. , 378 (1999) pp. 233–267 |
| [a17] | M. Brady, A. Leonard, D.I. Pullin, "Regularized vortex sheet evolution in three dimensions" J. Comput. Phys. , 146 (1998) pp. 520–45 |
Birkhoff-Rott equation. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Birkhoff-Rott_equation&oldid=18626