Bipolar coordinates

The numbers and which are connected with the Cartesian orthogonal coordinates and by the formulas

where . The coordinate lines are two families of circles 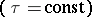with poles and and the (half-c)ircles orthogonal with these .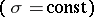

Figure: b016470a

The Lamé coefficients are:

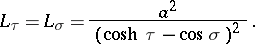The Laplace operator is:

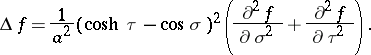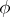Bipolar coordinates in space (bispherical coordinates) are the numbers and , which are connected with the orthogonal Cartesian coordinates 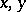and by the formulas:

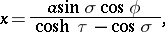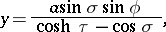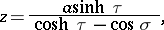where 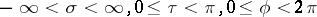. The coordinate surfaces are spheres (), the surfaces obtained by rotation of arcs of circles () and half-planes passing through the -axis. The system of bipolar coordinates in space is formed by rotating the system of bipolar coordinates on the plane around the 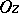-axis.

The Lamé coefficients are:

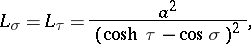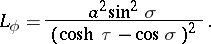The Laplace operator is:

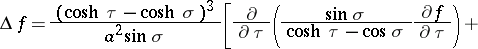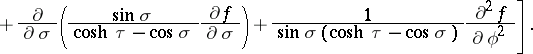References

[1]	E. Madelung, "Die mathematischen Hilfsmittel des Physikers" , Springer (1957)

References

[a1]	O. Veblen, J.H.C. Whitehead, "The foundations of differential geometry" , Cambridge Univ. Press (1932)