Binary Lie algebra
From Encyclopedia of Mathematics
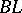 -algebra
-algebra
A linear algebra 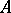 over a field
over a field 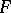 any two elements of which generate a Lie subalgebra. The class of all binary Lie algebras over a given field
any two elements of which generate a Lie subalgebra. The class of all binary Lie algebras over a given field 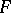 generates a variety which, if the characteristic of
generates a variety which, if the characteristic of 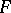 is different from 2, is given by the system of identities
is different from 2, is given by the system of identities
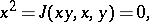 | (*) |
where
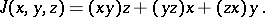 |
If the characteristic of 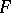 is 2 and its cardinal number is not less than 4, the class of binary Lie algebras can be defined not only by the system of identities (*), but also by the identity
is 2 and its cardinal number is not less than 4, the class of binary Lie algebras can be defined not only by the system of identities (*), but also by the identity
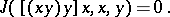 |
The tangent algebra of an analytic local alternative loop is a binary Lie algebra and vice versa.
References
| [1] | A.I. Mal'tsev, "Analytic loops" Mat. Sb. , 36 (78) : 3 (1955) pp. 569–575 (In Russian) |
| [2] | A.T. Gainov, "Binary Lie algebras of characteristic two" Algebra and Logic , 8 : 5 (1969) pp. 287–297 Algebra i Logika , 8 : 5 (1969) pp. 505–522 |
How to Cite This Entry:
Binary Lie algebra. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Binary_Lie_algebra&oldid=18121
Binary Lie algebra. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Binary_Lie_algebra&oldid=18121
This article was adapted from an original article by A.T. Gainov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article