Bieberbach-Eilenberg functions
in the disc 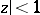
The class 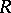 of functions
of functions 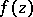 , regular in the disc
, regular in the disc 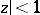 , which have an expansion of the form
, which have an expansion of the form
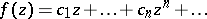 | (1) |
and which satisfy the condition
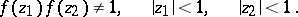 |
This class of functions is a natural extension of the class 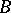 of functions
of functions 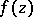 , regular in the disc
, regular in the disc 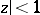 , with an expansion (1) and such that
, with an expansion (1) and such that 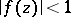 for
for 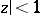 . The class of univalent functions (cf. Univalent function) in
. The class of univalent functions (cf. Univalent function) in 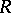 is denoted by
is denoted by 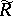 . The functions in
. The functions in 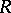 were named after L. Bieberbach [1], who showed that for
were named after L. Bieberbach [1], who showed that for 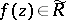 the inequality
the inequality
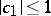 | (2) |
is valid, while equality holds only for the function 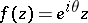 , where
, where 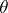 is real, and after S. Eilenberg [2], who proved that the inequality (2) is valid for the whole class
is real, and after S. Eilenberg [2], who proved that the inequality (2) is valid for the whole class 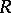 . It was shown by W. Rogosinski [3] that every function in
. It was shown by W. Rogosinski [3] that every function in 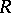 is subordinate (cf. Subordination principle) to some function in
is subordinate (cf. Subordination principle) to some function in 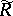 . Inequality (2) yields the following sharp inequality for
. Inequality (2) yields the following sharp inequality for 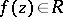 :
:
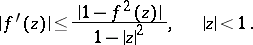 | (3) |
The following bound on the modulus of a function in 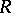 has been obtained: If
has been obtained: If 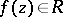 , then
, then
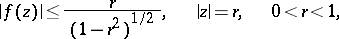 | (4) |
and (4) becomes an equality only for the functions 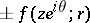 , where
, where 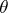 is real and
is real and
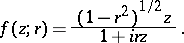 |
The method of the extremal metric (cf. Extremal metric, method of the) provided the solution of the problem of the maximum and minimum of 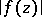 in the class
in the class 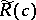 of functions in
of functions in 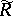 with a fixed value
with a fixed value 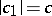 ,
, 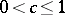 , in the expansion (1): For
, in the expansion (1): For 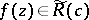 ,
, 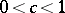 , the following sharp inequalities are valid:
, the following sharp inequalities are valid:
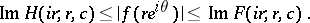 | (5) |
Here the functions 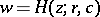 and
and 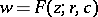 map the disc
map the disc 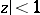 onto domains which are symmetric with respect to the imaginary axis of the
onto domains which are symmetric with respect to the imaginary axis of the 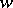 -plane, and the boundaries of which belong to the union of the closures of certain trajectories or orthogonal trajectories of a quadratic differential in the
-plane, and the boundaries of which belong to the union of the closures of certain trajectories or orthogonal trajectories of a quadratic differential in the 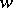 -plane with a certain symmetry in the distribution of the zeros and poles [4], [5]. Certain optimal results for functions in
-plane with a certain symmetry in the distribution of the zeros and poles [4], [5]. Certain optimal results for functions in 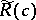 were obtained by the simultaneous use of the method of the extremal metric and the symmetrization method [4].
were obtained by the simultaneous use of the method of the extremal metric and the symmetrization method [4].
Many results obtained for the functions in the classes 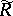 and
and 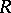 are consequences of corresponding results for systems of functions mapping the disc
are consequences of corresponding results for systems of functions mapping the disc 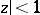 onto disjoint domains [6]. The analogue of
onto disjoint domains [6]. The analogue of 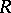 for a finitely-connected domain
for a finitely-connected domain 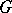 without isolated boundary points and not containing the point
without isolated boundary points and not containing the point 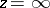 , is the class
, is the class 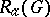 ,
, 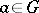 , of functions
, of functions 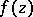 regular in
regular in 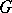 and satisfying the conditions
and satisfying the conditions 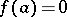 ,
, 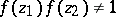 , where
, where 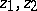 are arbitrary points in
are arbitrary points in 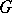 . The class
. The class 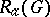 extends the class
extends the class 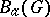 of functions
of functions 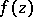 , regular in
, regular in 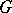 and such that
and such that 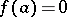 ,
, 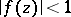 in
in 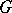 . The following sharp estimate is an extension of the result of Bieberbach–Eilenberg and of inequality (3) to functions of class
. The following sharp estimate is an extension of the result of Bieberbach–Eilenberg and of inequality (3) to functions of class 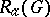 : If
: If 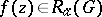 , then
, then
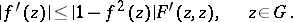 |
where 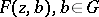 , is that function in
, is that function in 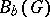 for which
for which 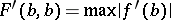 in this class.
in this class.
References
| [1] | L. Bieberbach, "Ueber einige Extremalprobleme im Gebiete der konformen Abbildung" Math. Ann. , 77 (1916) pp. 153–172 |
| [2] | S. Eilenberg, "Sur quelques propriétés topologiques de la surface de sphère" Fund. Math. , 25 (1935) pp. 267–272 |
| [3] | W. Rogosinski, "On a theorem of Bieberbach–Eilenberg" J. London Math. Soc. (1) , 14 (1939) pp. 4–11 |
| [4] | J.A. Jenkins, "Univalent functions and conformal mappings" , Springer (1958) |
| [5] | J.A. Jenkins, "On Bieberbach–Eilenberg functions III" Trans. Amer. Math. Soc. , 119 : 2 (1965) pp. 195–215 |
| [6] | N.A. Lebedev, "The area principle in the theory of univalent functions" , Moscow (1975) (In Russian) |
Comments
References
| [a1] | P.L. Duren, "Univalent functions" , Springer (1983) pp. Chapt. 10 |
Bieberbach-Eilenberg functions. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Bieberbach-Eilenberg_functions&oldid=22121