Bicategory
(update), weak  -category
-category
A  -category [a7], [a8], [a14], [a19], [a22] is a category
-category [a7], [a8], [a14], [a19], [a22] is a category  consisting of objects
consisting of objects  and arrows
and arrows  together with
together with  -arrows
-arrows  , which can be displayed as
, which can be displayed as

Figure: b120230a
and has vertical and horizontal composition operations

Figure: b120230b

Figure: b120230c
These compositions are required to be associative and unital; moreover, horizontal composition must preserve vertical units and the following interchange law is imposed:
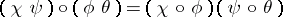 |

Figure: b120230d
The basic example of a  -category is
-category is 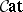 , whose objects are (small) categories, whose arrows are the functors (cf. also Functor), and whose
, whose objects are (small) categories, whose arrows are the functors (cf. also Functor), and whose  -arrows are natural transformations. Indeed, the basic "five rules" for composition of natural transformations appeared in [a11], Appendix.
-arrows are natural transformations. Indeed, the basic "five rules" for composition of natural transformations appeared in [a11], Appendix.
There is a weaker notion of  -category which occurs in practice. A weak
-category which occurs in practice. A weak  -category or bicategory [a1] consists of the data and conditions of a
-category or bicategory [a1] consists of the data and conditions of a  -category except that the associativity and unital equalities for horizontal composition are replaced by the extra data of invertible natural families of
-category except that the associativity and unital equalities for horizontal composition are replaced by the extra data of invertible natural families of  -arrows
-arrows
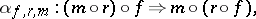 |
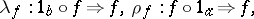 |
called associativity and unital constraints, such that the associativity pentagon (or  -cocycle condition)
-cocycle condition)
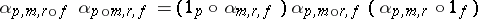 |
and unit triangle (or normalization condition)
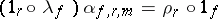 |
are imposed. In some of the recent literature, bicategories are called  -categories and
-categories and  -categories are called strict
-categories are called strict  -categories.
-categories.
A monoidal category  can be identified with the one-object bicategory
can be identified with the one-object bicategory  whose arrows are the objects of
whose arrows are the objects of  , whose
, whose  -arrows are the arrows of
-arrows are the arrows of 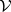 , whose horizontal composition is the tensor product of
, whose horizontal composition is the tensor product of 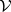 , and whose vertical composition is the composition of
, and whose vertical composition is the composition of 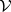 .
.
There is a bicategory 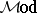 whose objects are (small) categories and whose arrows are modules [a31], [a34] (called pro-functors or distributors in [a2], and bimodules in [a21]) between categories.
whose objects are (small) categories and whose arrows are modules [a31], [a34] (called pro-functors or distributors in [a2], and bimodules in [a21]) between categories.
An arrow 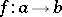 in a bicategory is called an equivalence when there is an arrow
in a bicategory is called an equivalence when there is an arrow 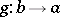 such that there are invertible
such that there are invertible  -arrows
-arrows 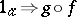 and
and  . A weak
. A weak  -groupoid is a bicategory in which each
-groupoid is a bicategory in which each  -arrow is invertible and each arrow is an equivalence. A
-arrow is invertible and each arrow is an equivalence. A  -groupoid is a
-groupoid is a  -category with all arrows and
-category with all arrows and  -arrows invertible. For each space
-arrows invertible. For each space 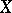 , there is a homotopy
, there is a homotopy  -groupoid,
-groupoid, 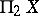 whose objects are the points of
whose objects are the points of  ; it contains the information of the fundamental groupoid
; it contains the information of the fundamental groupoid 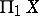 and the homotopy groups
and the homotopy groups 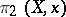 for each
for each 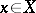 (cf. also Homotopy group; Crossed module; Crossed complex; Fundamental group). An early application of
(cf. also Homotopy group; Crossed module; Crossed complex; Fundamental group). An early application of  -categories to homotopy theory occurs in [a9]. In fact, Ch. Ehresmann [a7] defined double categories and double groupoids, which generalize
-categories to homotopy theory occurs in [a9]. In fact, Ch. Ehresmann [a7] defined double categories and double groupoids, which generalize  -categories in that they have two types of arrows (see [a19]), and these also have proved important in homotopy theory [a5].
-categories in that they have two types of arrows (see [a19]), and these also have proved important in homotopy theory [a5].
While many examples occur naturally as bicategories rather than  -categories, there is a coherence theorem asserting that every bicategory is equivalent (in the appropriate sense) to a
-categories, there is a coherence theorem asserting that every bicategory is equivalent (in the appropriate sense) to a  -category [a23], [a12].
-category [a23], [a12].
There are several purely categorical motivations for the development of bicategory theory. The first is to study bicategories following the theory of categories but taking account of the  -dimensionality; this is the spirit of [a10], [a14], [a18], [a29]. A given concept in category theory typically has several generalizations, stemming from the fact that equalities between arrows can be replaced by
-dimensionality; this is the spirit of [a10], [a14], [a18], [a29]. A given concept in category theory typically has several generalizations, stemming from the fact that equalities between arrows can be replaced by  -arrow constraints (lax generalization), by invertible
-arrow constraints (lax generalization), by invertible  -arrow constraints (pseudo-generalization), or by keeping the equalities; further equalities are required on the constraints. A bicategory can thus be regarded as a pseudo-category, an equivalence as a pseudo-isomorphism, and a stack (a "champ" in French) as a pseudo-sheaf. In lax cases there are also choices of direction for the equality-breaking constraints. All this applies to functors: there are lax functors (also called morphisms) and pseudo-functors (also called homomorphisms) between bicategories; there are
-arrow constraints (pseudo-generalization), or by keeping the equalities; further equalities are required on the constraints. A bicategory can thus be regarded as a pseudo-category, an equivalence as a pseudo-isomorphism, and a stack (a "champ" in French) as a pseudo-sheaf. In lax cases there are also choices of direction for the equality-breaking constraints. All this applies to functors: there are lax functors (also called morphisms) and pseudo-functors (also called homomorphisms) between bicategories; there are  -functors between
-functors between  -categories having equality constraints. This also applies to limits, adjunctions, Kan extensions, etc. [a10], [a14]. One can use the fact that
-categories having equality constraints. This also applies to limits, adjunctions, Kan extensions, etc. [a10], [a14]. One can use the fact that  -categories are categories with homs enriched in
-categories are categories with homs enriched in 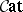 , that is,
, that is, 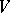 -categories where
-categories where 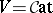 [a8]. Some laxness is even accounted for in this way: lax limits are enriched limits for a suitable weight (or index) [a28].
[a8]. Some laxness is even accounted for in this way: lax limits are enriched limits for a suitable weight (or index) [a28].
A second motivation comes from the fact that bicategories are "monoidal categories with several objects" . Included in this is the study of categories enriched in a bicategory which leads to a unification of category theory, sheaf theory, Boolean-valued logic, and the theory of metric spaces (cf. Metric space) [a38], [a31], [a34], [a3], [a24]. The generalization of Cauchy completion (cf. also Cauchy sequence) from the case of metric spaces is fundamental [a21].
A third impetus is the formalization of properties of the bicategory 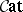 (as in the part of category theory which abstracts properties of the category
(as in the part of category theory which abstracts properties of the category 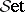 of sets) allowing the use of bicategories as organizational tools for studying categories with extra structure (in the way that categories themselves organize sets with structure). This leads to the study of arrow categories [a13], adjunctions [a17], monads (also called triples; cf. Triple) [a26], Kan extensions [a37], [a27] factorization systems (cf. also
of sets) allowing the use of bicategories as organizational tools for studying categories with extra structure (in the way that categories themselves organize sets with structure). This leads to the study of arrow categories [a13], adjunctions [a17], monads (also called triples; cf. Triple) [a26], Kan extensions [a37], [a27] factorization systems (cf. also 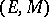 -factorization system in a category) [a31], [a32], [a33], [a6], etc., as concepts belonging within a fixed bicategory. Familiar constructions (such as comma categories and Eilenberg–Moore categories for monads) made with these concepts turn out to be limits of the kind arising in other motivations. In this spirit, one can mimic the construction of
-factorization system in a category) [a31], [a32], [a33], [a6], etc., as concepts belonging within a fixed bicategory. Familiar constructions (such as comma categories and Eilenberg–Moore categories for monads) made with these concepts turn out to be limits of the kind arising in other motivations. In this spirit, one can mimic the construction of 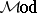 from
from 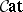 starting with a bicategory (satisfying certain exactness conditions) much as one constructs a category of relations in a regular category or topos [a29], [a6], [a25]. The size needs of category theory add extra challenges to the subject [a27], [a37].
starting with a bicategory (satisfying certain exactness conditions) much as one constructs a category of relations in a regular category or topos [a29], [a6], [a25]. The size needs of category theory add extra challenges to the subject [a27], [a37].
Low-dimensional topology enters bicategory theory from two dual directions. The commutative diagrams familiar in a category (cf. also Diagram) laxify in a bicategory to  -dimensional diagrams with
-dimensional diagrams with  -arrows in the regions; and these diagrams, if well formed, can be evaluated, using the compositions, to yield a unique
-arrows in the regions; and these diagrams, if well formed, can be evaluated, using the compositions, to yield a unique  -arrow called the pasted composite of the diagram [a1], [a14], [a19]. Two-dimensional graph-like structures called computads were designed to formalize pasting [a28]. The planar Poincaré-dual view replaces pasting diagrams with string diagrams; the
-arrow called the pasted composite of the diagram [a1], [a14], [a19]. Two-dimensional graph-like structures called computads were designed to formalize pasting [a28]. The planar Poincaré-dual view replaces pasting diagrams with string diagrams; the  -arrows label nodes, the arrows label strings (intervals embedded in the Euclidean plane), and the objects label regions [a16], [a36]. The planar geometry of string diagrams under deformation is faithful to the algebra of bicategories. See also Higher-dimensional category; Bicategory.
-arrows label nodes, the arrows label strings (intervals embedded in the Euclidean plane), and the objects label regions [a16], [a36]. The planar geometry of string diagrams under deformation is faithful to the algebra of bicategories. See also Higher-dimensional category; Bicategory.
References
| [a1] | J. Bénabou, "Introduction to bicategories" , Lecture Notes Math. , 47 , Springer (1967) pp. 1–77 |
| [a2] | J. Bénabou, "Les distributeurs" Sem. Math. Pure Univ. Catholique de Louvain , 33 (1973) |
| [a3] | R. Betti, A. Carboni, R. Walters, "Variation through enrichment" J. Pure Appl. Algebra , 29 (1983) pp. 109–127 |
| [a4] | G.J. Bird, G.M. Kelly, A.J. Power, R. Street, "Flexible limits for  -categories" J. Pure Appl. Algebra , 61 (1989) pp. 1–27 -categories" J. Pure Appl. Algebra , 61 (1989) pp. 1–27 |
| [a5] | R. Brown, "Higher dimensional group theory" R. Brown (ed.) T.L. Thickstun (ed.) , Low dimensional topology , Lecture Notes London Math. Soc. , 48 , Cambridge Univ. Press (1982) pp. 215–238 |
| [a6] | A. Carboni, S. Johnson, R. Street, D. Verity, "Modulated bicategories" J. Pure Appl. Algebra , 94 (1994) pp. 229–282 |
| [a7] | C. Ehresmann, "Catégories et structures" , Dunod (1965) |
| [a8] | S. Eilenberg, G.M. Kelly, "Closed categories" , Proc. Conf. Categorical Algebra, La Jolla , Springer (1966) pp. 421–562 |
| [a9] | P. Gabriel, M. Zisman, "Calculus of fractions and homotopy theory" , Ergebn. Math. Grenzgeb. , 35 , Springer (1967) |
| [a10] | J. Giraud, "Cohomologie non abélienne" , Springer (1971) |
| [a11] | R. Godement, "Topologie algébrique et théorie des faisceaux" , Hermann (1964) |
| [a12] | R. Gordon, A.J. Power, R. Street, "Coherence for tricategories" , Memoirs , 117 , Amer. Math. Soc. (1995) pp. 558 |
| [a13] | J.W. Gray, "Report on the meeting of the Midwest Category Seminar in Zürich" , Lecture Notes Math. , 195 , Springer (1971) pp. 248–255 |
| [a14] | J.W. Gray, "Formal category theory: adjointness for  -categories" , Lecture Notes Math. , 391 , Springer (1974) -categories" , Lecture Notes Math. , 391 , Springer (1974) |
| [a15] | M. Hakim, "Topos annelés et schémas relatifs" , Ergebn. Math. Grenzgeb. , 64 , Springer (1972) |
| [a16] | A. Joyal, R. Street, "The geometry of tensor calculus I" Adv. Math. , 88 (1991) pp. 55–112 |
| [a17] | G.M. Kelly, "Adjunction for enriched categories" , Lecture Notes Math. , 106 , Springer (1969) pp. 166–177 |
| [a18] | G.M. Kelly, "An abstract approach to coherence" , Lecture Notes Math. , 281 , Springer (1972) pp. 106–147 |
| [a19] | G.M. Kelly, R. Street, "Review of the elements of  -categories" , Lecture Notes Math. , 420 , Springer (1974) pp. 75–103 -categories" , Lecture Notes Math. , 420 , Springer (1974) pp. 75–103 |
| [a20] | F.W. Lawvere, "The category of categories as a foundation for mathematics" , Proc. Conf. Categorical Algebra, La Jolla , Springer (1966) pp. 1–20 |
| [a21] | F.W. Lawvere, "Metric spaces, generalised logic, and closed categories" Rend. Sem. Mat. Fis. Milano , 43 (1974) pp. 135–166 |
| [a22] | S. MacLane, "Categories for the working mathematician" , Graduate Texts Math. , 5 , Springer (1971) |
| [a23] | S. MacLane, R. Paré, "Coherence for bicategories and indexed categories" J. Pure Appl. Algebra , 37 (1985) pp. 59–80 |
| [a24] | A. Pitts, "Applications of sup-lattice enriched category theory to sheaf theory" Proc. London Math. Soc. , (3)57 (1988) pp. 433–480 |
| [a25] | R.D. Rosebrugh, R.J. Wood, "Proarrows and cofibrations" J. Pure Appl. Algebra , 53 (1988) pp. 271–296 |
| [a26] | R. Street, "The formal theory of monads" J. Pure Appl. Algebra , 2 (1972) pp. 149–168 |
| [a27] | R. Street, "Elementary cosmoi 1" , Lecture Notes Math. , 420 , Springer (1974) pp. 134–180 |
| [a28] | R. Street, "Limits indexed by category-valued  -functors" J. Pure Appl. Algebra , 8 (1976) pp. 149–181 -functors" J. Pure Appl. Algebra , 8 (1976) pp. 149–181 |
| [a29] | R. Street, "Fibrations in bicategories" Cah. Topol. Géom. Diff. , 21; 28 (1980; 1987) pp. 111–160; 53–56 |
| [a30] | R. Street, "Conspectus of variable categories" J. Pure Appl. Algebra , 21 (1981) pp. 307–338 |
| [a31] | R. Street, "Cauchy characterization of enriched categories" Rend. Sem. Mat. Fis. Milano , 51 (1981) pp. 217–233 |
| [a32] | R. Street, "Two dimensional sheaf theory" J. Pure Appl. Algebra , 23 (1982) pp. 251–270 |
| [a33] | R. Street, "Characterization of bicategories of stacks" , Lecture Notes Math. , 962 , Springer (1982) pp. 282–291 |
| [a34] | R. Street, "Enriched categories and cohomology" Quaest. Math. , 6 (1983) pp. 265–283 |
| [a35] | R. Street, "Categorical structures" M. Hazewinkel (ed.) , Handbook of Algebra , I , Elsevier (1996) pp. 529–577 |
| [a36] | R. Street, "Higher categories, strings, cubes and simplex equations" Appl. Categorical Struct. , 3 (1995) pp. 29–77 and 303 |
| [a37] | R. Street, R.F.C. Walters, "Yoneda structures on  -categories" J. Algebra , 50 (1978) pp. 350–379 -categories" J. Algebra , 50 (1978) pp. 350–379 |
| [a38] | R.F.C. Walters, "Sheaves on sites as Cauchy-complete categories" J. Pure Appl. Algebra , 24 (1982) pp. 95–102 |
Bicategory. Ross Street (originator), Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Bicategory&oldid=19168