Difference between revisions of "Bezout theorem"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
||
| Line 12: | Line 12: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> | + | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> E. Bezout, "Théorie génerale des équations algébriques" , Paris (1779)</TD></TR></table> |
| Line 20: | Line 20: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> | + | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> I.R. Shafarevich, "Basic algebraic geometry" , Springer (1977) pp. Chapt. 4, Sect. 2 (Translated from Russian) {{MR|0447223}} {{ZBL|0362.14001}} </TD></TR></table> |
Revision as of 21:50, 30 March 2012
Bezout's theorem on the division of a polynomial by a linear binomial: The remainder of the division of the polynomial
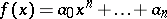 |
by the binomial 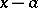 is
is 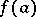 . It is assumed that the coefficients of the polynomials are contained in a certain commutative ring with a unit element, e.g. in the field of real or complex numbers. A consequence of Bezout's theorem is the following: A number
. It is assumed that the coefficients of the polynomials are contained in a certain commutative ring with a unit element, e.g. in the field of real or complex numbers. A consequence of Bezout's theorem is the following: A number 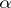 is a root of the polynomial
is a root of the polynomial 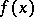 if and only if
if and only if 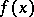 is divisible by the binomial
is divisible by the binomial 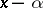 without remainder.
without remainder.
Bezout's theorem on homogeneous equations: If a system of  homogeneous equations in
homogeneous equations in 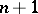 unknowns
unknowns
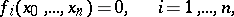 | (*) |
has only a finite number of non-proportional non-zero solutions in an algebraically closed field containing the coefficients of the system, then the number of these solutions counted according to their multiplicity is equal to the product of the degrees of the equations. The multiplicity of the solutions is, by definition, the intersection index (in algebraic geometry) of the hypersurfaces (*) at the respective point. The theorem is called after E. Bezout [1], who studied systems of algebraic equations of higher degrees.
References
| [1] | E. Bezout, "Théorie génerale des équations algébriques" , Paris (1779) |
Comments
References
| [a1] | I.R. Shafarevich, "Basic algebraic geometry" , Springer (1977) pp. Chapt. 4, Sect. 2 (Translated from Russian) MR0447223 Zbl 0362.14001 |
Bezout theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Bezout_theorem&oldid=11972