Betti number

-dimensional Betti number 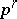of a complex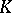

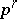The rank of the -dimensional Betti group with integral coefficients. For each the Betti number is a topological invariant of the polyhedron which realizes the complex 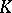, and it indicates the number of pairwise non-homological (over the rational numbers) cycles in it. For instance, for the sphere :

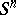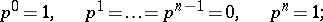for the projective plane :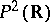

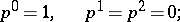for the torus :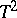

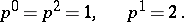For an -dimensional complex 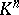the sum

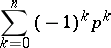is equal to its Euler characteristic. Betti numbers were introduced by E. Betti [1].

References

[1]	E. Betti, Ann. Mat. Pura Appl. , 4 (1871) pp. 140–158

References

[a1]	E.H. Spanier, "Algebraic topology" , McGraw-Hill (1966)