Beta-distribution
A continuous probability distribution concentrated on  with density
with density
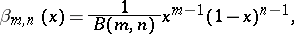 | (1) |
where the parameters  are non-negative and the normalizing factor
are non-negative and the normalizing factor  is Euler's beta-function
is Euler's beta-function
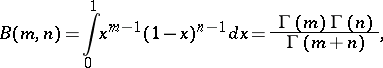 |
where  is the gamma-function. The distribution function is expressed as the incomplete beta-function
is the gamma-function. The distribution function is expressed as the incomplete beta-function
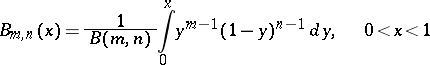 |
(this function has been tabulated, see [1], [2]). The moments of the beta-distribution are given by the formulas
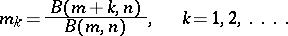 |
In particular, the mathematical expectation and the variance are  and
and 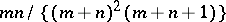 , respectively. If
, respectively. If  and
and 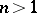 , the density curve
, the density curve  has a single mode at the point
has a single mode at the point 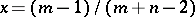 and vanishes at the ends of the interval. If either
and vanishes at the ends of the interval. If either 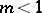 or
or 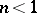 , one ordinate at the end of the graph becomes infinite, and if both
, one ordinate at the end of the graph becomes infinite, and if both 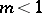 and
and 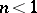 , both ordinates at the ends of the interval are infinite and the curve is U-shaped. If
, both ordinates at the ends of the interval are infinite and the curve is U-shaped. If 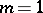 and
and 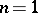 the beta-distribution reduces to the uniform distribution on the interval
the beta-distribution reduces to the uniform distribution on the interval 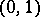 . Another special case of the beta-distribution is the so-called arcsine distribution:
. Another special case of the beta-distribution is the so-called arcsine distribution:
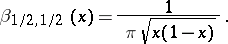 |
If one substitutes  in (1), then one obtains a distribution having the density
in (1), then one obtains a distribution having the density
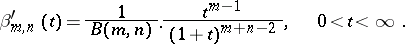 | (2) |
This distribution is called a beta-distribution of the second kind, as distinct from the beta-distribution (1). The distributions (1) and (2) correspond to "type I" and "type VI" distributions in the system of Pearson curves. An important case of generation of a beta-distribution is the following: If 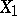 and
and 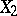 are independent and have gamma-distributions (cf. Gamma-distribution) with respective parameters
are independent and have gamma-distributions (cf. Gamma-distribution) with respective parameters 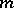 and
and  , then the random variable
, then the random variable  will have a beta-distribution with density
will have a beta-distribution with density 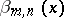 . This fact to a large extent explains the role played by beta-distributions in various applications, in particular in mathematical statistics: The distributions of several important statistics are reducible to beta-distributions. For instance, the distribution function of the
. This fact to a large extent explains the role played by beta-distributions in various applications, in particular in mathematical statistics: The distributions of several important statistics are reducible to beta-distributions. For instance, the distribution function of the 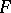 -relationship
-relationship
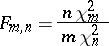 |
(the random variable 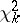 has a
has a  -distribution with
-distribution with 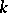 degrees of freedom) is expressed by the formula
degrees of freedom) is expressed by the formula
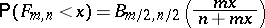 |
(the values of the 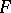 -distribution are usually calculated with the aid of tables of beta-functions). The beta-distribution function also allows one to compute the values of the binomial distribution functions, in view of the relationship
-distribution are usually calculated with the aid of tables of beta-functions). The beta-distribution function also allows one to compute the values of the binomial distribution functions, in view of the relationship
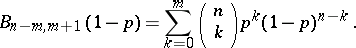 |
Beta-distributions are used in fields other than mathematical statistics; thus, the density of the beta-distribution is the weight function for the system of orthogonal Jacobi polynomials.
References
| [1] | L.N. Bol'shev, N.V. Smirnov, "Tables of mathematical statistics" , Libr. math. tables , 46 , Nauka (1983) (In Russian) (Processed by L.S. Bark and E.S. Kedrova) |
| [2] | K. Pearson, "Tables of the incomplete beta-function" , Cambridge Univ. Press (1932) |
Beta-distribution. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Beta-distribution&oldid=16107