Best quadrature formula
optimal quadrature formula
An approximate integration formula that guarantees the minimum error for a given class of functions, relative to all formulas of a specified type. As an example, consider the quadrature formula
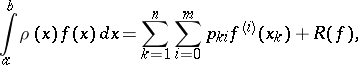 | (*) |
where 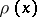 is a weight function. The remainder (error) term
is a weight function. The remainder (error) term 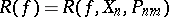 depends both on the function
depends both on the function 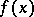 , and on the vector
, and on the vector 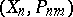 consisting of the interpolation nodes
consisting of the interpolation nodes 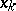 (it is usually assumed that
(it is usually assumed that 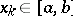 ) and the coefficients
) and the coefficients 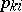 ,
, 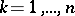 ;
;  . Fixing
. Fixing 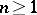 and
and 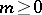 , let
, let 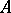 denote some set of vectors
denote some set of vectors 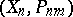 (and hence also some set of quadrature formulas), defined by some restrictions on the interpolation nodes and coefficients (in particular, one might consider the set
(and hence also some set of quadrature formulas), defined by some restrictions on the interpolation nodes and coefficients (in particular, one might consider the set 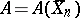 of coefficients
of coefficients  for a fixed node vector
for a fixed node vector  ). Let
). Let 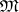 be some class of functions
be some class of functions 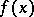 , it being assumed that the integral and the sum in (*) exist. The best quadrature formula of type (*) for the class
, it being assumed that the integral and the sum in (*) exist. The best quadrature formula of type (*) for the class 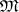 relative to the set
relative to the set 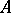 is defined by a vector
is defined by a vector 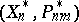 for which
for which
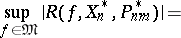 |
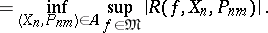 |
The construction of best quadrature formulas is intimately connected with certain problems in spline approximation; in many cases it reduces to minimizing the norm of a monospline (see [1]). Best quadrature formulas, together with sharp estimates for the remainder term, are known for many important classes of continuous and differentiable functions. From a more general point of view, the problem of finding best quadrature formulas and the corresponding errors for a class 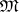 may be viewed as the problem of optimal recovery of a functional
may be viewed as the problem of optimal recovery of a functional
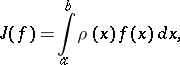 |
where 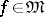 , on the basis of the information
, on the basis of the information 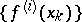 ,
, 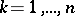 ;
; 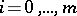 . The concept of a best quadrature formula generalizes in a natural way to functions of several variables (cubature formulas).
. The concept of a best quadrature formula generalizes in a natural way to functions of several variables (cubature formulas).
References
| [1] | S.M. Nikol'skii, "Quadrature formulae" , H.M. Stationary Office , London (1966) (Translated from Russian) |
| [2] | N.M. Krylov, "Approximate calculation of integrals" , Macmillan (1962) (Translated from Russian) |
| [3] | P.J. Laurent, "Approximation et optimisation" , Hermann (1972) |
| [4] | A.A. Zhensykbaev, "Monosplines of minimal norm and quadrature formulas" Uspekhi Mat. Nauk , 36 : 4 (1981) pp. 107–159 (In Russian) |
Comments
The terminology "best formula" is often encountered in the literature on numerical analysis, but, as was observed in [a2], p. 75, it should be taken with a large dose of salt, because, after all, any quadrature formula, no matter how the weights 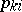 and the nodes
and the nodes 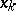 are chosen, will exactly integrate an infinite-dimensional family of functions.
are chosen, will exactly integrate an infinite-dimensional family of functions.
A few recent textbooks are listed below.
References
| [a1] | H. Brass, "Quadraturverfahren" , Vandenhoeck & Ruprecht (1977) |
| [a2] | P.J. Davis, P. Rabinowitz, "Methods of numerical integration" , Acad. Press (1984) |
| [a3] | H. Engels, "Numerical quadrature and cubature" , Acad. Press (1980) |
Best quadrature formula. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Best_quadrature_formula&oldid=13603