Best linear method
With respect to the approximation of elements in a given set  , the linear method that yields the smallest error among all linear methods. In a normed linear space
, the linear method that yields the smallest error among all linear methods. In a normed linear space  , a linear method for the approximation of elements
, a linear method for the approximation of elements  by elements of a fixed subspace
by elements of a fixed subspace  is represented by a linear operator that maps the entire space
is represented by a linear operator that maps the entire space  , or some linear manifold containing
, or some linear manifold containing  , into
, into  . If
. If  is the set of all such operators, a best linear method for
is the set of all such operators, a best linear method for  (if it exists) is defined by an operator
(if it exists) is defined by an operator 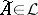 for which
for which
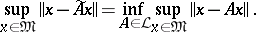 |
The method defined by an operator 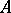 in
in 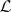 will certainly be a best linear method for
will certainly be a best linear method for 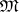 relative to the approximating set
relative to the approximating set 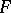 if, for all
if, for all 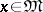 ,
,
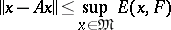 |
(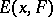 is the best approximation of
is the best approximation of  by
by  ) and if, moreover, for all
) and if, moreover, for all 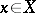 ,
,
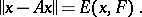 |
The latter is certainly true if 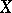 is a Hilbert space,
is a Hilbert space,  is an
is an  -dimensional subspace of
-dimensional subspace of 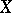 ,
, 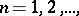 and
and  is the orthogonal projection onto
is the orthogonal projection onto 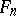 , i.e.
, i.e.
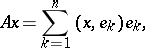 |
where 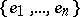 is an orthonormal basis in
is an orthonormal basis in 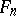 .
.
Let 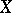 be a Banach space of functions defined on the entire real line, with a translation-invariant norm:
be a Banach space of functions defined on the entire real line, with a translation-invariant norm: 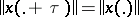 (this condition holds, e.g. for the norms of the spaces
(this condition holds, e.g. for the norms of the spaces 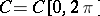 and
and  ,
, 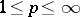 , of
, of 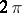 -periodic functions); let
-periodic functions); let 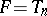 be the subspace of trigonometric polynomials of order
be the subspace of trigonometric polynomials of order  . There exist best linear methods (relative to
. There exist best linear methods (relative to 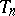 ) for a class
) for a class 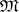 of functions
of functions 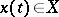 that contains
that contains 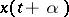 for any
for any 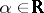 whenever it contains
whenever it contains 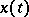 . An example is the linear method
. An example is the linear method
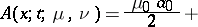 | (*) |
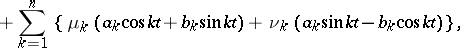 |
where 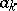 and
and 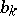 are the Fourier coefficients of
are the Fourier coefficients of 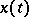 relative to the trigonometric system, and
relative to the trigonometric system, and 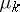 and
and 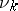 are numbers.
are numbers.
Now consider the classes 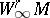 (and
(and  ),
), 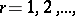 of
of 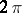 -periodic functions
-periodic functions 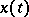 whose derivatives
whose derivatives 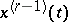 are locally absolutely continuous and whose derivatives
are locally absolutely continuous and whose derivatives 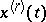 are bounded in norm in
are bounded in norm in 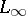 (respectively, in
(respectively, in 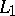 ) by a number
) by a number 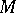 . For these classes, best linear methods of the type (*) yield the same error (over the entire class) in the metric of
. For these classes, best linear methods of the type (*) yield the same error (over the entire class) in the metric of  (respectively,
(respectively, 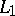 ) as the best approximation by a subspace
) as the best approximation by a subspace 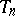 ; the analogous assertion is true for these classes with any rational number
; the analogous assertion is true for these classes with any rational number 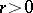 (interpreting the derivatives
(interpreting the derivatives 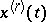 in the sense of Weyl). For integers
in the sense of Weyl). For integers 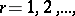 best linear methods of type (*) have been constructed using only the coefficients
best linear methods of type (*) have been constructed using only the coefficients 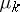 (all
(all 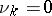 ).
).
If 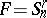 is the subspace of
is the subspace of 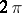 -periodic polynomial splines of order
-periodic polynomial splines of order  and defect 1 with respect to the partition
and defect 1 with respect to the partition  ,
, 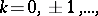 then a best linear method for the classes
then a best linear method for the classes 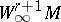 (and
(and 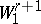 ),
), 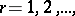 is achieved in
is achieved in 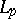 ,
, 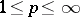 (resp. in
(resp. in 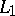 ) by splines in
) by splines in  interpolating the function
interpolating the function 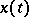 at the points
at the points 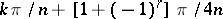 .
.
References
| [1] | N.I. [N.I. Akhiezer] Achiezer, "Theory of approximation" , F. Ungar (1956) (Translated from Russian) |
| [2] | N.P. Korneichuk, "Extremal problems in approximation theory" , Moscow (1976) (In Russian) |
| [3] | V.M. Tikhomirov, "Some problems in approximation theory" , Moscow (1976) (In Russian) |
Comments
References
| [a1] | H. Kiesewetter, "Vorlesungen über lineare Approximation" , Deutsch. Verlag Wissenschaft. (1973) |
| [a2] | J.R. Rice, "The approximation of functions" , 1. Linear theory , Addison-Wesley (1964) |
Best linear method. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Best_linear_method&oldid=19004