Bessel processes
A family of continuous Markov processes (cf. Markov process)  taking values in
taking values in 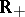 , parametrized by their dimension
, parametrized by their dimension  .
.
When 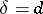 is an integer,
is an integer,  may be represented as the Euclidean norm of Brownian motion in
may be represented as the Euclidean norm of Brownian motion in  . Let
. Let 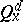 be the law of the square, starting from
be the law of the square, starting from  , of such a process
, of such a process  , considered as a random variable taking values in
, considered as a random variable taking values in 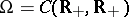 . This law is infinitely divisible (cf. [a6] and Infinitely-divisible distribution). Hence, there exists a unique family
. This law is infinitely divisible (cf. [a6] and Infinitely-divisible distribution). Hence, there exists a unique family 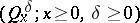 of laws on
of laws on  such that
such that
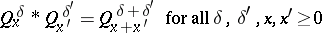 | (a1) |
( indicates the convolution of probabilities on
indicates the convolution of probabilities on  ), which coincides with the family
), which coincides with the family 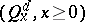 , for integer dimensions
, for integer dimensions 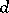 .
.
The process of coordinates 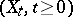 on
on  , under
, under 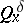 , satisfies the equation
, satisfies the equation
 | (a2) |
with 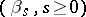 a one-dimensional Brownian motion. Equation (a2) admits a unique strong solution, with values in
a one-dimensional Brownian motion. Equation (a2) admits a unique strong solution, with values in 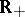 . Call its square root a
. Call its square root a 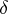 -dimensional Bessel process.
-dimensional Bessel process.
Bessel processes also appear naturally in the Lamperti representation of the process 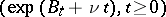 , where
, where 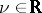 and
and 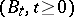 denotes a one-dimensional Brownian motion. This representation is:
denotes a one-dimensional Brownian motion. This representation is:
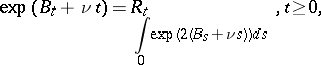 | (a3) |
where 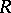 is a
is a 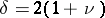 -dimensional Bessel process. This representation (a3) has a number of consequences, among which absolute continuity properties of the laws
-dimensional Bessel process. This representation (a3) has a number of consequences, among which absolute continuity properties of the laws 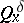 as
as 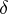 varies and
varies and 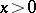 is fixed, and also the fact that a power of a Bessel process is another Bessel process, up to a time-change.
is fixed, and also the fact that a power of a Bessel process is another Bessel process, up to a time-change.
Special representations of Bessel processes of dimensions one and three, respectively, have been obtained by P. Lévy, as 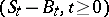 , and by J. Pitman as
, and by J. Pitman as 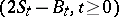 , where
, where 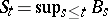 , and
, and  is a one-dimensional Brownian motion.
is a one-dimensional Brownian motion.
Finally, the laws of the local times of 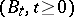 considered up to first hitting times, or inverse local times, can be expressed in terms of
considered up to first hitting times, or inverse local times, can be expressed in terms of 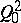 and
and 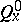 , respectively: this is the content of the celebrated Ray–Knight theorems (1963; [a1], [a5]) on Brownian local times. These theorems have been extended to a large class of processes, including real-valued diffusions.
, respectively: this is the content of the celebrated Ray–Knight theorems (1963; [a1], [a5]) on Brownian local times. These theorems have been extended to a large class of processes, including real-valued diffusions.
References
| [a1] | F.B. Knight, "Random walks and a sojourn density process of Brownian motion" Trans. Amer. Math. Soc. , 107 (1963) pp. 56–86 |
| [a2] | J.W. Pitman, "One-dimensional Brownian motion and the three-dimensional Bessel process" Adv. Applied Probab. , 7 (1975) pp. 511–526 |
| [a3] | J.W. Pitman, M. Yor, "Bessel processes and infinitely divisible laws" D. Williams (ed.) , Stochastic Integrals , Lecture Notes in Mathematics , 851 , Springer (1981) |
| [a4] | J.W. Pitman, M. Yor, "A decomposition of Bessel bridges" Z. Wahrscheinlichkeitsth. verw. Gebiete , 59 (1982) pp. 425–457 |
| [a5] | D.B. Ray, "Sojourn times of a diffusion process" Ill. J. Math. , 7 (1963) pp. 615–630 |
| [a6] | T. Shiga, S. Watanabe, "Bessel diffusions as a one-parameter family of one-dimensional diffusion processes" Z. Wahrscheinlichkeitsth. verw. Gebiete , 27 (1973) pp. 37–46 |
| [a7] | D. Revuz, M. Yor, "Continuous martingales and Brownian motion" , Springer (1994) (Edition: Second) |
Bessel processes. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Bessel_processes&oldid=17022