Bessel potential space
fractional Sobolev space, Liouville space
A Banach space of integrable functions or distributions on the  -dimensional Euclidean space
-dimensional Euclidean space  , which generalizes the ordinary Sobolev space of functions whose derivatives belong to
, which generalizes the ordinary Sobolev space of functions whose derivatives belong to  -classes, and their duals. If
-classes, and their duals. If 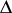 denotes the Laplace operator, the Bessel potential space
denotes the Laplace operator, the Bessel potential space  ,
,  ,
,  , can be defined as the space of functions (or distributions)
, can be defined as the space of functions (or distributions)  such that
such that  belongs to the Lebesgue space
belongs to the Lebesgue space 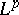 , normed by the corresponding Lebesgue norm. The operator
, normed by the corresponding Lebesgue norm. The operator 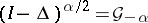 , which for
, which for  is a kind of fractional differentiation (cf. also Fractional integration and differentiation), is most easily defined by means of the Fourier transform. It corresponds, in fact, to multiplication of the Fourier transform of
is a kind of fractional differentiation (cf. also Fractional integration and differentiation), is most easily defined by means of the Fourier transform. It corresponds, in fact, to multiplication of the Fourier transform of 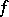 by
by 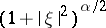 . The operator clearly has the group properties
. The operator clearly has the group properties  , and
, and 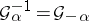 .
.
It is a theorem of A.P. Calderón that for positive integers  and
and 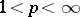 the space
the space  coincides (with equivalence of norms) with the Sobolev space
coincides (with equivalence of norms) with the Sobolev space 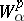 of functions all of whose derivatives (in the distributional, or weak sense) of order at most
of functions all of whose derivatives (in the distributional, or weak sense) of order at most  are functions in
are functions in  .
.
For 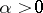 the elements of
the elements of  are themselves
are themselves  -functions, which can be represented as Bessel potentials of
-functions, which can be represented as Bessel potentials of  -functions. In fact, the function
-functions. In fact, the function 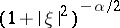 is then the Fourier transform of an integrable function, the Bessel kernel
is then the Fourier transform of an integrable function, the Bessel kernel 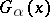 , and the operator
, and the operator  can be represented by a convolution with this kernel. In other words,
can be represented by a convolution with this kernel. In other words, 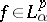 ,
, 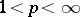 ,
, 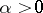 , if and only if there is a
, if and only if there is a  such that
such that  , where the integral is taken over all of
, where the integral is taken over all of 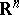 with respect to the Lebesgue measure.
with respect to the Lebesgue measure.
The kernel 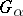 can be expressed explicitly by means of a modified Bessel function of the third kind (cf. also Bessel functions), also known as a Macdonald function, and for this reason the Bessel potentials were given their name by N. Aronszajn and K.T. Smith in 1961. More important than the exact expression for the kernel is the fact that it is a suitable modification of the (Marcel) Riesz kernel
can be expressed explicitly by means of a modified Bessel function of the third kind (cf. also Bessel functions), also known as a Macdonald function, and for this reason the Bessel potentials were given their name by N. Aronszajn and K.T. Smith in 1961. More important than the exact expression for the kernel is the fact that it is a suitable modification of the (Marcel) Riesz kernel 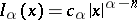 ,
, 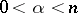 , whose Fourier transform is
, whose Fourier transform is 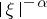 . The Bessel kernel has the same properties as the Riesz kernel for small
. The Bessel kernel has the same properties as the Riesz kernel for small  , but thanks to the fact that its Fourier transform behaves nicely at
, but thanks to the fact that its Fourier transform behaves nicely at  , it decays exponentially at infinity. In contrast to the Riesz kernel it is therefore an integrable function, and this is its main advantage.
, it decays exponentially at infinity. In contrast to the Riesz kernel it is therefore an integrable function, and this is its main advantage.
The spaces  appear naturally as interpolation spaces that are obtained from Sobolev spaces by means of the complex interpolation method (cf. also Interpolation of operators). They are included in the more general scale of Lizorkin–Triebel spaces
appear naturally as interpolation spaces that are obtained from Sobolev spaces by means of the complex interpolation method (cf. also Interpolation of operators). They are included in the more general scale of Lizorkin–Triebel spaces 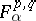 ; in fact,
; in fact,  (with equivalence of norms) for
(with equivalence of norms) for 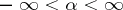 and
and  . This equivalence is a highly non-trivial result of so-called Littlewood–Paley type. Related to this are very useful representations by means of atoms.
. This equivalence is a highly non-trivial result of so-called Littlewood–Paley type. Related to this are very useful representations by means of atoms.
The Hilbert space 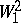 , also known as the Dirichlet space, and its generalizations
, also known as the Dirichlet space, and its generalizations 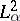 are intimately related to classical potential theory. The study of more general non-Hilbert spaces
are intimately related to classical potential theory. The study of more general non-Hilbert spaces  and
and  , motivated by investigations of non-linear partial differential equations, has lead to the creation of a new non-linear potential theory, and many of the results and concepts of the classical theory have been extended to the non-linear setting, sometimes in unexpected ways.
, motivated by investigations of non-linear partial differential equations, has lead to the creation of a new non-linear potential theory, and many of the results and concepts of the classical theory have been extended to the non-linear setting, sometimes in unexpected ways.
References
| [a1] | D.R. Adams, L.I. Hedberg, "Function spaces and potential theory" , Springer (1996) |
| [a2] | H. Triebel, "Theory of function spaces II" , Birkhäuser (1992) |
Bessel potential space. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Bessel_potential_space&oldid=16844