Bessel potential
A potential of the form
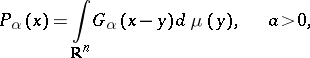 |
where  ,
,  are points in the Euclidean space
are points in the Euclidean space  ,
,  ;
;  is a Borel measure on
is a Borel measure on  ;
;
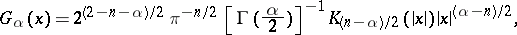 |
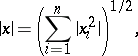 |
and  is the modified cylinder function (or Bessel function, cf. Cylinder functions) of the second kind of order
is the modified cylinder function (or Bessel function, cf. Cylinder functions) of the second kind of order  or the Macdonald function of order
or the Macdonald function of order  ;
;  is called a Bessel kernel.
is called a Bessel kernel.
The principal properties of the Bessel kernels 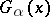 are the same as those of the Riesz kernels (cf. Riesz potential), viz., they are positive, continuous for
are the same as those of the Riesz kernels (cf. Riesz potential), viz., they are positive, continuous for  , can be composed
, can be composed
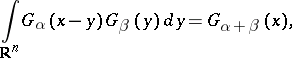 |
but, unlike the Riesz potentials, Bessel potentials are applicable for all  , since
, since
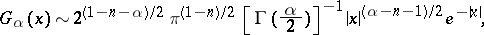 |
as  .
.
If  , where
, where 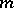 is a natural number, and the measure
is a natural number, and the measure 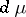 is absolutely continuous with square-integrable density
is absolutely continuous with square-integrable density 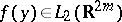 , the Bessel potentials satisfy the identities:
, the Bessel potentials satisfy the identities:
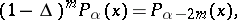 |
and
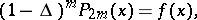 |
where 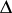 is the Laplace operator on
is the Laplace operator on  . In other words, the function
. In other words, the function  is a fundamental solution of the operator
is a fundamental solution of the operator  .
.
References
| [1] | S.M. Nikol'skii, "Approximation of functions of several variables and imbedding theorems" , Springer (1975) (Translated from Russian) |
| [2] | M. Aronszajn, K.T. Smith, "Theory of Bessel potentials I" Ann. Inst. Fourier (Grenoble) , 11 (1961) pp. 385–475 |
Comments
The function  is usually called the modified Bessel function of the third kind.
is usually called the modified Bessel function of the third kind.
Bessel potential. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Bessel_potential&oldid=13961