Berry-Esseen inequality
From Encyclopedia of Mathematics
An inequality giving an estimate of the deviation of the distribution function of a sum of independent random variables from the normal distribution function. Let 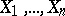 be independent random variables with the same distribution such that
be independent random variables with the same distribution such that
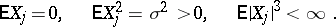 |
Let
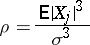 |
and
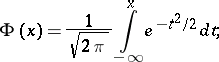 |
then, for any  ,
,
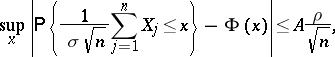 |
where 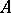 is an absolute positive constant. This result was obtained by A.C. Berry [1] and, independently, by C.G. Esseen [2].
is an absolute positive constant. This result was obtained by A.C. Berry [1] and, independently, by C.G. Esseen [2].
References
| [1] | A.C. Berry, "The accuracy of the Gaussian approximation to the sum of independent variables" Trans. Amer. Math. Soc. , 49 (1941) pp. 122–136 |
| [2] | C.G. Esseen, "On the Liapunoff limit of error in the theory of probability" Ark. Mat. Astr. Fysik , 28A : 2 (1942) pp. 1–19 |
| [3] | V.V. Petrov, "Sums of independent random variables" , Springer (1975) (Translated from Russian) |
Comments
The constant 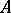 can be taken to be
can be taken to be 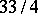 , cf. [a1], p. 515 ff.
, cf. [a1], p. 515 ff.
References
| [a1] | W. Feller, "An introduction to probability theory and its applications" , 2 , Wiley (1966) pp. 210 |
How to Cite This Entry:
Berry-Esseen inequality. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Berry-Esseen_inequality&oldid=16984
Berry-Esseen inequality. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Berry-Esseen_inequality&oldid=16984
This article was adapted from an original article by V.V. Petrov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article