Bernstein problem in mathematical genetics
Bernshtein problem
Let  be the simplex in
be the simplex in  spanned by the canonical basis
spanned by the canonical basis  . Any set of numbers
. Any set of numbers  (
( ) such that
) such that  and
and  defines a stochastic quadratic mapping
defines a stochastic quadratic mapping  by the formulas
by the formulas
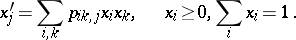 |
This mapping is called Bernstein (or stationary) if 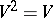 . The Bernstein problem is to explicitly describe all such mappings. This problem was posed by S.N. Bernshtein [a1] in order to create a mathematical foundation of population genetics. For
. The Bernstein problem is to explicitly describe all such mappings. This problem was posed by S.N. Bernshtein [a1] in order to create a mathematical foundation of population genetics. For 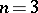 , this problem has been solved in [a2]. (For
, this problem has been solved in [a2]. (For 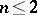 the problem is trivial.)
the problem is trivial.)
The classical Mendel mechanism of heredity defines a mapping
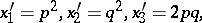 |
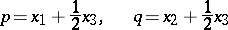 |
(the Hardy–Weinberg formulas, cf. [a5]). Biologically, 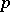 and
and 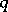 are the probabilities of an alternating pair of genes, say
are the probabilities of an alternating pair of genes, say 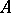 and
and  respectively, in a population where the individuals may be of genotypes
respectively, in a population where the individuals may be of genotypes 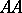 ,
, 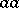 and
and 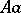 . Then
. Then 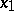 ,
, 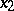 ,
, 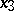 are the probabilities of these genotypes in a generation. If the next generation is formed by random mating, then the probabilities turn into
are the probabilities of these genotypes in a generation. If the next generation is formed by random mating, then the probabilities turn into 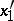 ,
, 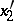 ,
, 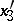 . As a result,
. As a result, 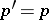 ,
, 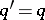 and then
and then 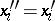 (
(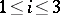 ), i.e. the Hardy–Weinberg mapping is stationary. Conversely, if for
), i.e. the Hardy–Weinberg mapping is stationary. Conversely, if for 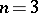 a stationary mapping
a stationary mapping 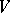 is such that
is such that  and all quadratic forms
and all quadratic forms  , then
, then 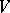 is a Hardy–Weinberg mapping (see [a2], [a6]). Thus, the only Mendelian heredity is stationary and such that all offsprings for the parental couple
is a Hardy–Weinberg mapping (see [a2], [a6]). Thus, the only Mendelian heredity is stationary and such that all offsprings for the parental couple 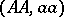 are
are 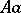 (and, in addition, such that all genotypes are present in the next generation).
(and, in addition, such that all genotypes are present in the next generation).
For any stochastic quadratic mapping 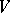 , the linear form
, the linear form 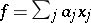 is called invariant if
is called invariant if  . The mapping
. The mapping 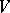 is called regular if there exists a family
is called regular if there exists a family 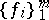 of invariant linear forms such that
of invariant linear forms such that 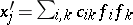 for certain constant coefficients
for certain constant coefficients 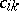 . The Hardy–Weinberg mapping is regular. Another interesting example is the quadrille mapping (see [a2], [a6]):
. The Hardy–Weinberg mapping is regular. Another interesting example is the quadrille mapping (see [a2], [a6]):
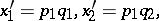 |
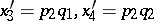 |
where
 |
 |
For the regular case, the Bernstein problem has been solved in [a6], [a8], [a9]. This is precisely the case when the stationarity is based on a system of genes (see [a7]). The genes correspond to the extremal rays of the cone of non-negative invariant linear forms. After a normalization, these forms are just the probabilities of the genes.
A standard genetical interpretation also requires 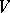 to be normal in the sense that:
to be normal in the sense that:
1) all 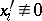 ;
;
2) for any pair 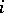 ,
, 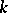 the quadratic forms
the quadratic forms  and
and 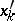 are not proportional;
are not proportional;
3) there is no pair 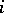 ,
,  such that all
such that all 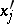 are functions of
are functions of 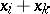 and of the remaining
and of the remaining 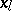 . If
. If  is normal together with its restrictions to all invariant faces of
is normal together with its restrictions to all invariant faces of  , then
, then 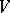 is called ultranormal. All stationary ultranormal mappings are regular [a13].
is called ultranormal. All stationary ultranormal mappings are regular [a13].
A non-regular stochastic Bernstein mapping appears already for 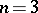 :
:
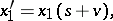 |
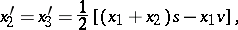 |
where  ,
, 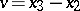 . Here, all invariant linear forms are trivial, i.e. proportional to
. Here, all invariant linear forms are trivial, i.e. proportional to  .
.
For the non-regular case there are some partial results for the Bernstein problem. In particular, the results cover the low dimensions 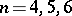 (cf. [a3], [a4], [a10]).
(cf. [a3], [a4], [a10]).
In the course of these investigations, Bernstein algebras were introduced as a powerful tool (see [a6], [a8] or Bernstein algebra). The theory of Bernstein algebras was subsequently developed by itself.
In the algebraic context, the Bernstein problem is to explicitly describe those Bernstein algebras which are stochastic with respect to the basis 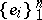 . The latter means that the product of every pair of basis vectors belongs to
. The latter means that the product of every pair of basis vectors belongs to  .
.
The Bernstein algebra corresponding to a regular mapping 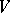 is regular by definition. This class is the most important from the genetics point of view.
is regular by definition. This class is the most important from the genetics point of view.
Another important tool in the study of the Bernstein problem is a topological structure on the set of essential faces of 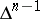 , the faces such that their intersections with the image of
, the faces such that their intersections with the image of 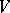 are non-empty [a11].
are non-empty [a11].
See [a12] for a systematic presentation of the results and methods regarding the Bernstein problem up to the middle of the 1980s.
References
| [a1] | S.N. Bernstein, "Mathematical problems in modern biology" Science in the Ukraine , 1 (1922) pp. 14–19 (In Russian) |
| [a2] | S.N. Bernstein, "Solution of a mathematical problem related to the theory of inheritance" Uchen. Zap. Nauch. Issl. Kafedr. Ukrain. , 1 (1924) pp. 83–115 (In Russian) |
| [a3] | S. Gonzáles, J.C. Gutiérrez, C. Martinez, "The Bernstein problem in dimension 5" J. Algebra , 177 (1995) pp. 676–697 |
| [a4] | J.C. Gutiérrez, "The Bernstein problem in dimension 6" J. Algebra , 185 (1996) pp. 420–439 |
| [a5] | G.H. Hardy, "Mendelian proportions in a mixed population" Science , 28 : 706 (1908) pp. 49–50 |
| [a6] | Y.I. Lyubich, "Basic concepts and theorems of evolutionary genetics for free populations" Russian Math. Surveys , 26 : 5 (1971) pp. 51–123 |
| [a7] | Y.I. Lyubich, "Analogues to the Hardy–Weinberg Law" Genetics , 9 : 10 (1973) pp. 139–144 (In Russian) |
| [a8] | Y.I. Lyubich, "Two-level Bernstein populations" Math. USSR Sb. , 24 : 1 (1974) pp. 593–615 |
| [a9] | Y.I. Lyubich, "Proper Bernstein populations" Probl. Inform. Transmiss. , Jan. (1978) pp. 228–235 |
| [a10] | Y.I. Lyubich, "Quasilinear Bernstein populations" Teor. Funct. Funct. Anal. Appl. , 26 (1976) pp. 79–84 |
| [a11] | Y.I. Lyubich, "A topological approach to a problem in mathematical genetics" Russian Math. Surveys , 34 : 6 (1979) pp. 60–66 |
| [a12] | Y.I. Lyubich, "Mathematical structures in population genetics" , Springer (1992) |
| [a13] | Y.I. Lyubich, "A new advance in the Bernstein problem in mathematical genetics" Preprint Inst. Math. Sci., SUNY Stony Brook , 9 (1996) pp. 1–33 |
Bernstein problem in mathematical genetics. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Bernstein_problem_in_mathematical_genetics&oldid=16709