Bernstein problem in differential geometry

It is a well-known and elementary fact in complex analysis that a bounded and holomorphic function on the whole plane must be a constant (cf. Liouville theorems). S.N. Bernstein proved an analogous result in differential geometry (cf. [a2]), saying that a smooth function defined on the whole plane and whose graph is a minimal surface, must be a constant (see Bernstein theorem). The classical Bernstein problem asks whether the corresponding result also holds for functions of variables, . More precisely, is it true that entire solutions (cf. also Entire function) of the minimal equation

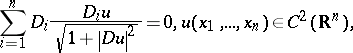where 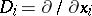, , must necessarily be a linear function? This equation is the condition that the mean curvature of the graph of the function in vanishes everywhere.

The answer to the above question is affirmative in the range 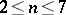; the proof of this is the result of the successive efforts of Bernstein [a2], W.H. Fleming [a7], [a8], E. DeGiorgi [a9], F. Almgren [a1], and J. Simons [a16]. On the other hand, a counterexample for 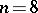, which in turn renders a counterexample for each 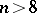by a standard construction, was obtained in 1969 by E. Bombieri, DeGiorgi and E. Giusti, cf. [a3]. The complete solution of the classical Bernstein problem constitutes, indeed, an exciting chapter of global differential geometry, involving geometric measure theory and non-linear analysis (cf. also Plateau problem).

Among the various generalizations of the above problem, the so-called spherical Bernstein problem is a natural and challenging one in the realm of global differential geometry. Let the 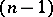-sphere 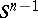be imbedded as a minimal hypersurface of the Euclidean n-sphere 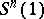. Is it necessarily an equator?

This problem is due to S.S. Chern (cf. [a5]; he also proposed it at the International Congress of Mathematicians at Nice (1970), cf. [a6]). The problem has, for example, a direct bearing on the possible local structures of isolated singularities of minimal hypersurfaces 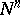in a general Riemannian manifold. Indeed, the (regular) tangent cone of 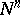at the singularity is a minimal cone in 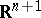, whose intersection with 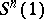is a minimal hypersurface.

By the Almgren–Calabi theorem [a1], [a4], an immersion (cf. Immersion of a manifold) of 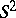into 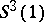must, in fact, be an equator. Thus, at least the beginning case 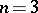of the spherical Bernstein problem was known to have a positive answer. However, no further progress was made until 1983, when Wu-yi Hsiang, in the framework of equivariant differential geometry, constructed infinitely many mutually non-congruent minimal imbeddings of 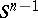into 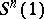, for each 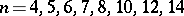(cf. [a11], [a12]). The basic ideas of this approach, which was initiated by Hsiang and H.B. Lawson [a10], is to choose an orthogonal representation 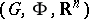with codimension-two principal orbits, and to search for solutions of the geometric problem which are invariant under the induced orthogonal transformation group 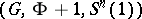. Thus, the original partial differential equation associated with the minimal hypersurface condition is reduced to an ordinary second-order differential equation on the -dimensional orbit space , which is geometrically a spherical lune. Here, the "closed" (in a certain sense) solution curves represent minimal hypersurfaces, and they will have the correct topology of 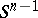thanks to the trivial summand added to .

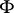During the 1980s, Hsiang and his collaborators obtained further results related to the spherical Bernstein problem, by investigating equivariant systems of the above type, as well as additional isoparametric foliations on 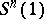. For instance, many new examples of imbedded as well as immersed minimal hyperspheres 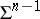in 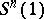have been constructed, and moreover, the stability of the singularity at the origin of the corresponding minimal cone 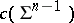in 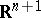has been investigated, see, e.g., [a13]. P. Tomter [a15] has shown the existence of a minimal and imbedded hypersphere 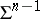in 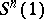which is not an equator, for each even . On the other hand, although the methods give infinitely many non-congruent minimal immersions of 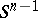for each 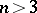, the problem of finding a non-equatorial imbedded sphere 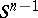in 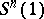for odd remains open.

Finally, as a generalization of the spherical Bernstein problem, it is also natural to replace the ambient space 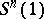by a simply-connected, compact symmetric space. See [a14] for some recent results in this direction.

References

[a1]	F.J. Almgren, Jr., "Some interior regularity theorems for minimal surfaces and an extension of the Bernstein's theorem" Ann. of Math. , 85 (1966) pp. 277–292
[a2]	S.N. Bernstein, "Sur une théorème de géometrie et ses applications aux dérivées partielles du type elliptique" Comm. Inst. Sci. Math. Mech. Univ. Kharkov , 15 (1915–17) pp. 38–45
[a3]	E. Bombieri, E. DeGiorgi, E. Giusti, "Minimal cones and the Bernstein problem" Invent. Math. , 7 (1969) pp. 243–268
[a4]	E. Calabi, "Minimal immersions of surfaces in euclidean spaces" J. Diff. Geom. , 1 (1967) pp. 111–125
[a5]	S.S. Chern, "Brief survey of minimal submanifolds" Tagungsbericht Oberwolfach (1969)
[a6]	S.S. Chern, "Differential geometry, its past and its future" , Actes Congres Intern. Mathem. , 1 (1970) pp. 41–53
[a7]	W.H. Fleming, "On the oriented Plateau problem" Rend. Circ. Mat. Palermo , II (1962) pp. 1–22
[a8]	W.H. Fleming, "Flat chains over a finite coefficient group" Trans. Amer. Math. Soc. , 121 (1966) pp. 160–186
[a9]	E. DeGiorgi, "Una estensione del teoreme di Bernstein" Ann. Sc. Norm. Sup. Pisa , 19 (1965) pp. 79–85
[a10]	W.Y. Hsiang, H.B. Lawson, Jr., "Minimal submanifolds of low cohomogeneity" J. Diff. Geom. , 5 (1971) pp. 1–38
[a11]	W.Y. Hsiang, "Minimal cones and the spherical Bernstein problem I" Ann. of Math. , 118 (1983) pp. 61–73
[a12]	W.Y. Hsiang, "Minimal cones and the spherical Bernstein problem II" Invent. Math. , 74 (1983) pp. 351–369
[a13]	W.Y. Hsiang, I. Sterling, "Minimal cones and the spherical Bernstein problem III" Invent. Math. , 85 (1986) pp. 223–247
[a14]	W.Y. Hsiang, W.T. Hsiang, P. Tomter, "On the existence of minimal hyperspheres in compact symmetric spaces" Ann. Sci. Ecole Norm. Sup. , 21 (1988) pp. 287–305
[a15]	P. Tomter, "The spherical Bernstein problem in even dimensions and related problems" Acta Math. , 158 (1987) pp. 189–212
[a16]	Simons, J., "Minimal varieties in Riemannian manifolds" Ann. of Math. , 88 (1968) pp. 62–105