Bernstein polynomials
Algebraic polynomials defined by the formula
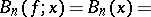 |
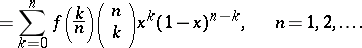 |
Introduced by S.N. Bernshtein in 1912 (cf. ). The sequence of Bernstein polynomials converges uniformly to a function 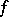 on the segment
on the segment 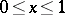 if
if 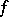 is continuous on this segment. For a function which is bounded by
is continuous on this segment. For a function which is bounded by 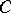 ,
, 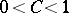 , with a discontinuity of the first kind,
, with a discontinuity of the first kind,
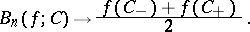 |
The equation
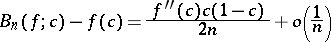 |
is valid if 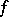 is twice differentiable at the point
is twice differentiable at the point  . If the
. If the 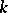 -th derivative
-th derivative 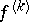 of the function is continuous on the segment
of the function is continuous on the segment 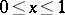 , the convergence
, the convergence
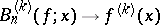 |
is uniform on this segment. A study was made ([1b], [5]) of the convergence of Bernstein polynomials in the complex plane if 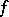 is analytic on the segment
is analytic on the segment 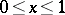 .
.
References
| [1a] | S.N. Bernshtein, , Collected works , 1 , Moscow (1952) pp. 105–106 |
| [1b] | S.N. Bernshtein, , Collected works , 2 , Moscow (1954) pp. 310–348 |
| [2] | V.L. Goncharov, "The theory of interpolation and approximation of functions" , Moscow (1954) (In Russian) |
| [3] | V.A. Baskakov, "An instance of a sequence of linear positive operators in the space of continuous functions" Dokl. Akad. Nauk SSSR , 113 : 2 (1957) pp. 249–251 (In Russian) |
| [4] | P.P. Korovkin, "Linear operators and approximation theory" , Hindushtan Publ. Comp. (1960) (Translated from Russian) |
| [5] | L.V. Kantorovich, Izv. Akad. Nauk SSSR Ser. Mat. , 8 (1931) pp. 1103–1115 |
Comments
There is also a multi-variable generalization: generalized Bernstein polynomials defined by the completely analogous formula
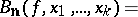 |
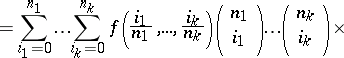 |
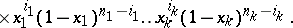 |
Here 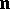 stands for the multi-index
stands for the multi-index 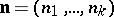 .
.
As in the one variable case these provide explicit polynomial approximants for the more-variable Weierstrass approximation and Stone–Weierstrass theorems. For the behaviour of Bernstein polynomials in the complex plane and applications to movement problems, cf. also [a3].
References
| [a1] | P.J. Davis, "Interpolation and approximation" , Dover, reprint (1975) pp. 108–126 |
| [a2] | T.J. Rivlin, "An introduction to the approximation of functions" , Dover, reprint (1981) |
| [a3] | G.G. Lorentz, "Bernstein polynomials" , Univ. Toronto Press (1953) |
Bernstein polynomials. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Bernstein_polynomials&oldid=46028