Bernstein inequality
Bernstein's inequality in probability theory is a more precise formulation of the classical Chebyshev inequality in probability theory, proposed by S.N. Bernshtein [1] in 1911; it permits one to estimate the probability of large deviations by a monotone decreasing exponential function (cf. Probability of large deviations). In fact, if the equations
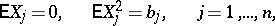 |
hold for the independent random variables 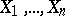 with
with
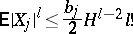 |
(where 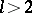 and
and 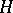 is a constant independent of
is a constant independent of 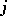 ), then the following inequality of Bernstein (where
), then the following inequality of Bernstein (where 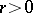 ) is valid for the sum
) is valid for the sum 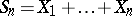 :
:
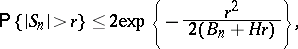 | (1) |
where 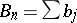 . For identically-distributed bounded random variables
. For identically-distributed bounded random variables 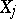 (
(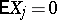 ,
, 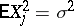 and
and 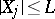 ,
, 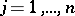 ) inequality (1) takes its simplest form:
) inequality (1) takes its simplest form:
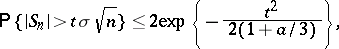 | (2) |
where 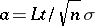 . A.N. Kolmogorov gave a lower estimate of the probability in (1). The Bernstein–Kolmogorov estimates are used, in particular, in proving the law of the iterated logarithm. Some idea of the accuracy of (2) may be obtained by comparing it with the approximate value of the left-hand side of (2) which is obtained by the central limit theorem in the form
. A.N. Kolmogorov gave a lower estimate of the probability in (1). The Bernstein–Kolmogorov estimates are used, in particular, in proving the law of the iterated logarithm. Some idea of the accuracy of (2) may be obtained by comparing it with the approximate value of the left-hand side of (2) which is obtained by the central limit theorem in the form
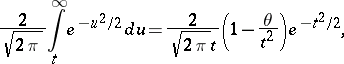 |
where 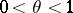 . Subsequent to 1967, Bernstein's inequalities were extended to include multi-dimensional and infinite-dimensional cases.
. Subsequent to 1967, Bernstein's inequalities were extended to include multi-dimensional and infinite-dimensional cases.
References
| [1] | S.N. Bernshtein, "Probability theory" , Moscow-Leningrad (1946) (In Russian) |
| [2] | A.N. [A.N. Kolmogorov] Kolmogoroff, "Ueber das Gesetz des iterierten Logarithmus" Math. Ann. , 101 (1929) pp. 126–135 |
| [3] | W. Hoeffding, "Probability inequalities for sums of independent random variables" J. Amer. Statist. Assoc. , 58 (1963) pp. 13–30 |
| [4] | V.V. Yurinskii, "Exponential inequalities for sums of random vectors" J. Multivariate Anal. , 6 (1976) pp. 473–499 |
A.V. Prokhorov
Bernstein's inequality for the derivative of a trigonometric or algebraic polynomial gives an estimate of this derivative in terms of the polynomial itself. If 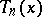 is a trigonometric polynomial of degree not exceeding
is a trigonometric polynomial of degree not exceeding  and if
and if
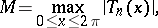 |
then the following inequalities are valid for all  (cf. [1]):
(cf. [1]):
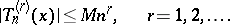 |
These estimates cannot be improved, since the number 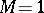 for
for
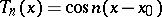 |
is sharp:
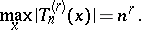 |
Bernstein's inequality for trigonometric polynomials is a special case of the following theorem [2]: If 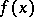 is an entire function of order
is an entire function of order 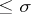 and if
and if
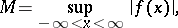 |
then one has
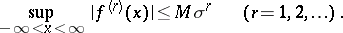 |
Bernstein's inequality for an algebraic polynomial has the following form [1]: If the polynomial
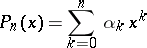 |
satifies the condition
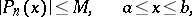 |
then its derivative 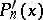 has the property
has the property
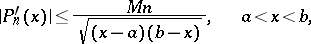 |
which cannot be improved. As was noted by S.N. Bernshtein [1], this inequality is a consequence of the proof of the Markov inequality given by A.A. Markov.
Bernstein's inequalities are in fact employed in proving converse theorems in the theory of approximation of functions. There are a number of generalizations of Bernstein's inequality, in particular for entire functions in several variables.
References
| [1] | S.N. [S.N. Bernshtein] Bernstein, "Sur l'ordre de la meilleure approximation des fonctions continues par des polynômes" Acad. R. Belgique, Cl. Sci. Mém. Coll. 4. Sér. II , 4 (1922) |
| [2] | S.N. [S.N. Bernshtein] Bernstein, "Sur une propriété des fonctions entières" C.R. Acad. Sci. Paris , 176 (1923) pp. 1603–1605 |
| [3] | S.M. Nikol'skii, "Approximation of functions of several variables and imbedding theorems" , Springer (1975) (Translated from Russian) |
N.P. KorneichukV.P. Motornyi
Comments
References
| [a1] | I.P. Natanson, "Constructive function theory" , 1–3 , F. Ungar (1964–1965) (Translated from Russian) |
| [a2] | G.G. Lorentz, "Approximation of functions" , Holt, Rinehart & Winston (1966) pp. Chapt. 2 |
Bernstein inequality. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Bernstein_inequality&oldid=15217