Bernoulli method
A method for finding the real root of algebraic equations of the type
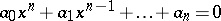 | (*) |
with the largest modulus (absolute value). The method was proposed by D. Bernoulli [1] and is based on the following principle. Let 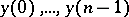 be random numbers and let the values of
be random numbers and let the values of 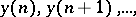 be calculated by the following difference equation:
be calculated by the following difference equation:
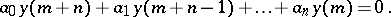 |
In general, as 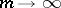 , the expression
, the expression 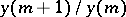 tends to the value of the root of equation (*) with the largest modulus.
tends to the value of the root of equation (*) with the largest modulus.
References
| [1] | D. Bernoulli, Comm. Acad. Sci. Imper. Petropolitanae , 3 , Petropolis (1732) pp. 62–69 |
| [2] | E.T. Whittaker, G. Robinson, "Mathematische Bearbeitung von Resultaten der Observation" , Leningrad-Moscow (1935) (In Russian; translated from German) |
Comments
The expression 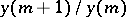 tends to the root of largest modulus only if this root is simple and if no other roots of the same maximum modulus occur. If not, then one can proceed as follows (cf. [a1]). Let there be one (not necessarily real) root
tends to the root of largest modulus only if this root is simple and if no other roots of the same maximum modulus occur. If not, then one can proceed as follows (cf. [a1]). Let there be one (not necessarily real) root 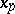 of largest modulus, with multiplicity
of largest modulus, with multiplicity 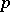 . Then the solution of the linear difference equation for
. Then the solution of the linear difference equation for 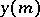 is
is
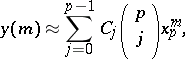 |
as 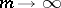 . This expression is the solution of a linear difference equation with characteristic polynomial
. This expression is the solution of a linear difference equation with characteristic polynomial 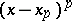 , so that
, so that 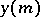 satisfies the linear difference equation
satisfies the linear difference equation
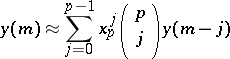 | (a1) |
as 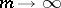 . If
. If 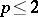 , then this equation can be solved explicitly in
, then this equation can be solved explicitly in 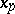 , otherwise (a1) is rewritten with
, otherwise (a1) is rewritten with 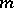 replaced by
replaced by 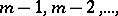 and the resulting equations are solved in
and the resulting equations are solved in 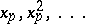 .
.
If two roots 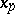 and
and 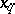 (of multiplicity
(of multiplicity 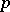 and
and 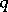 ) of the same maximum modulus occur, then
) of the same maximum modulus occur, then 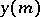 satisfies, as
satisfies, as 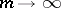 , a linear difference equation with
, a linear difference equation with  as characteristic polynomial, and (a1) must be replaced by the corresponding difference equation of order
as characteristic polynomial, and (a1) must be replaced by the corresponding difference equation of order 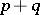 .
.
References
| [a1] | F.B. Hildebrand, "Introduction to numerical analysis" , McGraw-Hill (1956) |
| [a2] | A.S. Householder, "The numerical treatment of a single nonlinear equation" , McGraw-Hill (1970) |
Bernoulli method. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Bernoulli_method&oldid=12883