Bernoulli experiment
of size 
The special case of a statistical experiment 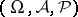 (cf. also Probability space; Statistical experiments, method of) consisting of a set
(cf. also Probability space; Statistical experiments, method of) consisting of a set 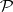 of probability measures
of probability measures 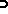 on a
on a 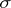 -algebra
-algebra 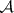 of subsets of a set
of subsets of a set  , where
, where  (
(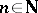 ,
, 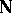 the set of natural numbers),
the set of natural numbers), 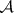 is the
is the 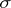 -algebra of all subsets of
-algebra of all subsets of 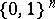 and
and 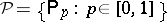 . Here, the probability measure
. Here, the probability measure 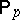 describes the probability
describes the probability
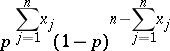 |
for a given probability 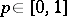 of success that
of success that 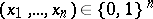 will be observed. Clearly, decision-theoretical procedures associated with Bernoulli experiments are based on the sum
will be observed. Clearly, decision-theoretical procedures associated with Bernoulli experiments are based on the sum  of observations
of observations 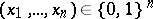 because of the corresponding sufficient and complete data reduction (cf. [a2] and [a3]). Therefore, uniformly most powerful, as well as uniformly most powerful unbiased, level tests for one-sided and two-sided hypotheses about the probability
because of the corresponding sufficient and complete data reduction (cf. [a2] and [a3]). Therefore, uniformly most powerful, as well as uniformly most powerful unbiased, level tests for one-sided and two-sided hypotheses about the probability  of success are based on
of success are based on 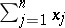 (cf. [a2]; see also Statistical hypotheses, verification of). Moreover, based on the quadratic loss function, the sample mean
(cf. [a2]; see also Statistical hypotheses, verification of). Moreover, based on the quadratic loss function, the sample mean
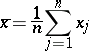 |
is admissible on account of the Rao–Cramér inequality (cf. [a3]) and the estimator (cf. also Statistical estimator)
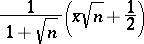 |
is minimax by means of equalizer decision rules (cf. [a2]). Furthermore, the Lehmann–Scheffé theorem implies that 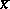 is a uniform minimum-variance unbiased estimator (an UMVU estimator; cf. also Unbiased estimator) for the probability
is a uniform minimum-variance unbiased estimator (an UMVU estimator; cf. also Unbiased estimator) for the probability  of success (cf. [a2] and [a3]).
of success (cf. [a2] and [a3]).
All UMVU estimators, as well as all unbiased estimators of zero, might be characterized in connection with Bernoulli experiments by introducing the following notion for general statistical experiments 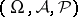 : A
: A 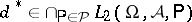 , being square-integrable for all
, being square-integrable for all 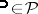 , is called an UMVU estimator if
, is called an UMVU estimator if
 |
for all 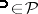 . The covariance method tells that
. The covariance method tells that 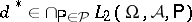 is a UMVU estimator if and only if
is a UMVU estimator if and only if 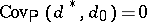 ,
, 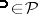 , for all unbiased estimators
, for all unbiased estimators 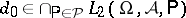 of zero, i.e. if
of zero, i.e. if  ,
, 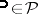 (cf. [a3]). In particular, the covariance method implies the following properties of UMVU estimators:
(cf. [a3]). In particular, the covariance method implies the following properties of UMVU estimators:
i) (uniqueness) 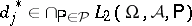 ,
, 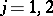 , UMVU estimators with
, UMVU estimators with 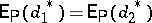 ,
, 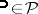 , implies
, implies 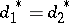
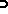 -a.e. for all
-a.e. for all  .
.
ii) (linearity)  , UMVU estimators,
, UMVU estimators, 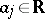 (
(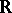 the set of real numbers),
the set of real numbers),  , implies that
, implies that 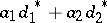 is also an UMVU estimator.
is also an UMVU estimator.
iii) (multiplicativity) 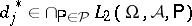 ,
, 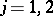 , UMVU estimators with
, UMVU estimators with 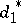 or
or 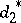 bounded, implies that
bounded, implies that 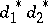 is also an UMVU estimator.
is also an UMVU estimator.
iv) (closedness) 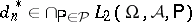 ,
, 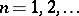 , UMVU estimators satisfying
, UMVU estimators satisfying 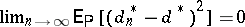 for some
for some  and all
and all 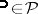 implies that
implies that 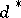 is an UMVU estimator.
is an UMVU estimator.
In the special case of a Bernoulli experiment of size  one arrives by the property of uniqueness i) and the property of linearity ii), together with an argument based on interpolation polynomials, at the following characterization of UMVU estimators:
one arrives by the property of uniqueness i) and the property of linearity ii), together with an argument based on interpolation polynomials, at the following characterization of UMVU estimators: 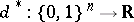 is a UMVU estimator if and only if one of the following conditions is valid:
is a UMVU estimator if and only if one of the following conditions is valid:
v) 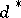 is a polynomial in
is a polynomial in  ,
, 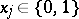 ,
,  , of degree not exceeding
, of degree not exceeding  ;
;
vi) 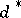 is symmetric (permutation invariant).
is symmetric (permutation invariant).
Moreover, the set of all real-valued parameter functions 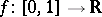 admitting some
admitting some 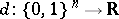 with
with 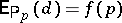 ,
, 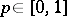 , coincides with the set consisting of all polynomials in
, coincides with the set consisting of all polynomials in 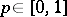 of degree not exceeding
of degree not exceeding  . In particular,
. In particular, 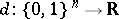 is an unbiased estimator of zero if and only if its symmetrization
is an unbiased estimator of zero if and only if its symmetrization 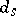 , defined by
, defined by
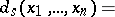 |
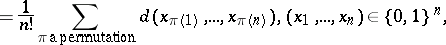 |
vanishes. Therefore, the set  consisting of all estimators
consisting of all estimators 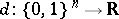 is equal to the direct sum
is equal to the direct sum 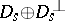 , where
, where 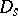 , stands for
, stands for 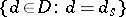 and
and 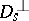 is equal to
is equal to 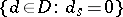 . In particular,
. In particular, 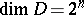 ,
, 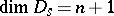 and
and 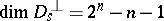 .
.
If one is interested, in connection with general statistical experiments 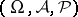 , only in locally minimum-variance unbiased estimators at some
, only in locally minimum-variance unbiased estimators at some 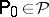 , one might start from
, one might start from 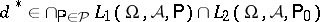 satisfying
satisfying
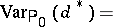 |
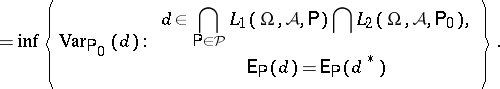 |
Then the covariance method yields again the properties of uniqueness, linearity and closedness (with respect to 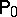 ), whereas the property of multiplicativity does not hold, in general, for locally minimum-variance unbiased estimators; this can be illustrated by infinite Bernoulli experiments, where the probability
), whereas the property of multiplicativity does not hold, in general, for locally minimum-variance unbiased estimators; this can be illustrated by infinite Bernoulli experiments, where the probability 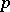 of success is equal to
of success is equal to 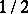 , as follows.
, as follows.
Let ( ) be the special statistical experiment with
) be the special statistical experiment with  ,
,  coinciding with the set of all subsets of
coinciding with the set of all subsets of 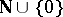 , and
, and  being the set of all binomial distributions
being the set of all binomial distributions 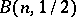 with integer-valued parameter
with integer-valued parameter 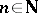 and probability of success
and probability of success 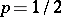 (cf. also Binomial distribution). Then the covariance method, together with an argument based on interpolation polynomials, yields the following characterization of locally optimal unbiased estimators:
(cf. also Binomial distribution). Then the covariance method, together with an argument based on interpolation polynomials, yields the following characterization of locally optimal unbiased estimators: 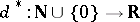 is locally optimal at
is locally optimal at 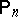 for all
for all  (
(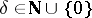 fixed) among all estimators
fixed) among all estimators 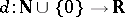 with
with 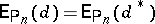 ,
, 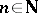 , if and only if
, if and only if 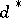 is a polynomial in
is a polynomial in 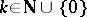 of degree not exceeding
of degree not exceeding 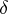 . In particular,
. In particular, 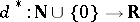 is a UMVU estimator if and only if
is a UMVU estimator if and only if 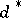 is already deterministic. Moreover, the property of multiplicativity of locally optimal unbiased estimators is not valid.
is already deterministic. Moreover, the property of multiplicativity of locally optimal unbiased estimators is not valid.
There is also the following version of the preceding characterization of locally optimal unbiased estimators for 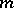 realizations of independent, identically distributed random variables with some binomial distribution
realizations of independent, identically distributed random variables with some binomial distribution 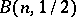 ,
, 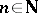 , as follows. Let
, as follows. Let  , let
, let  be the set of all subsets of
be the set of all subsets of  , let
, let 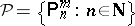 , where
, where 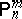 denotes the
denotes the 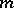 -fold direct product of
-fold direct product of 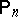 having the binomial distribution
having the binomial distribution 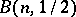 . Then
. Then 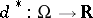 is locally optimal at
is locally optimal at 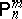 for all
for all 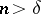 (
(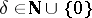 fixed) among all estimators
fixed) among all estimators  with
with  ,
,  , if
, if 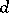 is a symmetric polynomial in
is a symmetric polynomial in 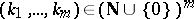 and a polynomial in
and a polynomial in 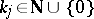 keeping the remaining variables
keeping the remaining variables 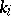 ,
, 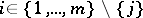 fixed,
fixed, 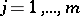 , of degree not exceeding
, of degree not exceeding 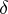 . In particular, for
. In particular, for 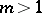 the sample mean
the sample mean
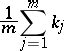 |
is not locally optimal at 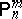 for any
for any 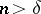 and some fixed
and some fixed 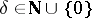 .
.
Finally, there are also interesting results about Bernoulli experiments of size  with varying probabilities of success, which, in connection with the randomized response model (cf. [a1]), have the form
with varying probabilities of success, which, in connection with the randomized response model (cf. [a1]), have the form 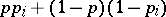 ,
, 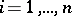 , with
, with 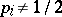 ,
,  , fixed and
, fixed and 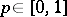 . Then there exists an UMVU estimator for
. Then there exists an UMVU estimator for 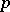 based on
based on 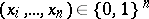 if and only if
if and only if 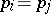 or
or 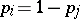 for all
for all  . In this case
. In this case
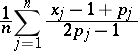 |
is a UMVU estimator for 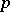 .
.
If the probabilities of success 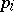 are functions
are functions 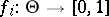 ,
, 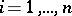 , with
, with 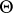 as parameter space, there exists a symmetric and sufficient data reduction of
as parameter space, there exists a symmetric and sufficient data reduction of 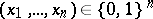 if and only if there are functions
if and only if there are functions 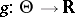 ,
, 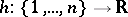 such that
such that
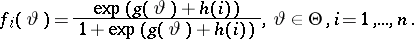 |
In particular, the sample mean is sufficient in this case.
References
| [a1] | A. Chaudhuri, R. Mukerjee, "Randomized response" , M. Dekker (1988) |
| [a2] | T.S. Ferguson, "Mathematical statistics: a decision theoretic approach" , Acad. Press (1967) |
| [a3] | E.L. Lehmann, "Theory of point estimation" , Wiley (1983) |
Bernoulli experiment. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Bernoulli_experiment&oldid=11211