Bernoulli automorphism
An automorphism of a measure space, which describes Bernoulli trials and their generalization — a sequence of independent trials with the same result and with the same probability distribution.
Let 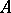 be the collection of all possible outcomes of a trial, and let the probability of the event
be the collection of all possible outcomes of a trial, and let the probability of the event 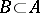 be given by the measure
be given by the measure  ; for a countable set
; for a countable set 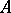 , denote its elements by
, denote its elements by  and their probabilities by
and their probabilities by 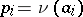 . The phase space of a Bernoulli automorphism is the direct product of a countable number of copies of the set
. The phase space of a Bernoulli automorphism is the direct product of a countable number of copies of the set 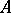 , i.e. the points of the phase space are infinite sequences
, i.e. the points of the phase space are infinite sequences 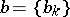 , where
, where 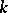 runs through the set of integers and each
runs through the set of integers and each 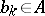 . The transformation
. The transformation 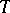 consists in shifting all members of each sequence one place to the left:
consists in shifting all members of each sequence one place to the left: 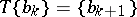 . The measure
. The measure 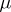 is defined as the direct product of a countable number of measures
is defined as the direct product of a countable number of measures  ; thus if
; thus if  is countable, then
is countable, then
 |
In this case, the entropy of the Bernoulli automorphism is 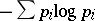 .
.
In ergodic theory, Bernoulli automorphisms (or, more exactly, the cascades generated by iteration of them) play the role of a standard example of a dynamical system, the behaviour of which displays statistical features. A Bernoulli automorphism is a 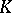 -automorphism but there exist
-automorphism but there exist  -automorphisms which are metrically non-isomorphic to a Bernoulli automorphism, even though many
-automorphisms which are metrically non-isomorphic to a Bernoulli automorphism, even though many 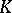 -automorphisms are metrically isomorphic to a Bernoulli automorphism. Two Bernoulli automorphisms are metrically isomorphic if and only if they have the same entropy . A Bernoulli automorphism is a quotient automorphism of any ergodic automorphism of a Lebesgue space with a larger entropy [2].
-automorphisms are metrically isomorphic to a Bernoulli automorphism. Two Bernoulli automorphisms are metrically isomorphic if and only if they have the same entropy . A Bernoulli automorphism is a quotient automorphism of any ergodic automorphism of a Lebesgue space with a larger entropy [2].
References
| [1a] | D. Ornstein, "Bernoulli shifts with the same entropy are isomorphic" Adv. Math. , 4 (1970) pp. 337–352 |
| [1b] | D.Ornstein, "A Kolmogorov automorphism that is not a Bernoulli shift" Matematika , 15 : 1 (1971) pp. 131–150 (In Russian) |
| [2] | Ya.G. Sinai, "On weak isomorphism of transformations with invariant measure" Mat. Sb. , 63 (105) : 1 (1964) pp. 23–42 (In Russian) |
Comments
A metric isomorphism between two Bernoulli automorphisms can be given by means of a finitary code ([a1], see also [a4]).
References
| [a1] | M. Keane, M. Smorodinsky, "Bernoulli schemes with the same entropy are finitarily isomorphic" Ann. of Math. , 109 (1979) pp. 397–406 |
| [a2] | M. Smorodinsky, "Ergodic theory, entropy" , Springer (1971) |
| [a3] | D. Ornstein, "Ergodic theory, randomness, and dynamical systems" , Yale Univ. Press (1974) |
| [a4] | I.P. [I.P. Kornfel'd] Cornfel'd, S.V. Fomin, Ya.G. Sinai, "Ergodic theory" , Springer (1982) (Translated from Russian) |
Bernoulli automorphism. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Bernoulli_automorphism&oldid=17876