Bergman-Weil representation
Bergman–Weil formula, Weil formula
An integral representation of holomorphic functions, obtained by S. Bergman [1] and A. Weil [2] and defined as follows. Let  be a domain of holomorphy in
be a domain of holomorphy in  , let the functions
, let the functions  be holomorphic in
be holomorphic in  and let
and let  compactly belong to
compactly belong to  . It is then possible to represent any function
. It is then possible to represent any function  holomorphic in
holomorphic in  and continuous on
and continuous on  at any point
at any point  by the formula:
by the formula:
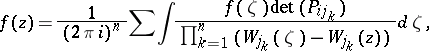 | (*) |
where the summation is performed over all  , while the integration is carried out over suitably-oriented
, while the integration is carried out over suitably-oriented  -dimensional surfaces
-dimensional surfaces  , forming the skeleton of the domain
, forming the skeleton of the domain 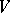 (cf. Analytic polyhedron),
(cf. Analytic polyhedron),  . Here the functions
. Here the functions  are holomorphic in the domain
are holomorphic in the domain  and are defined, in accordance with Hefer's lemma [3], by the equations
and are defined, in accordance with Hefer's lemma [3], by the equations
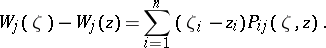 |
The integral representation (*) is called the Bergman–Weil representation.
The domains 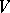 appearing in the Bergman–Weil representation are called Weil domains; an additional condition must usually be imposed, viz. that the ranks of the matrices
appearing in the Bergman–Weil representation are called Weil domains; an additional condition must usually be imposed, viz. that the ranks of the matrices 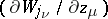 ,
,  ,
, 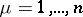 ,
, 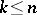 , on the corresponding sets
, on the corresponding sets
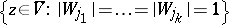 |
are maximal  for all
for all  (such Weil domains are called regular). The Weil domains in the Bergman–Weil representations may be replaced by analytic polyhedra
(such Weil domains are called regular). The Weil domains in the Bergman–Weil representations may be replaced by analytic polyhedra  compactly belonging to D,
compactly belonging to D,
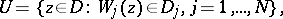 |
where the 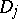 are bounded domains with piecewise-smooth boundaries
are bounded domains with piecewise-smooth boundaries 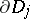 in the plane
in the plane  . The Bergman–Weil representation defines the value of a holomorphic function
. The Bergman–Weil representation defines the value of a holomorphic function 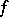 inside the analytic polyhedron
inside the analytic polyhedron 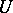 from the values of
from the values of 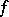 on the skeleton
on the skeleton 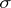 ; for
; for  the dimension of
the dimension of 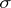 is strictly lower than that of
is strictly lower than that of 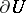 . If
. If 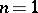 , analytic polyhedra become degenerate in a domain with piecewise-smooth boundary, the skeleton and the boundary become identical, and if, moreover,
, analytic polyhedra become degenerate in a domain with piecewise-smooth boundary, the skeleton and the boundary become identical, and if, moreover, 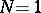 and
and  , then the Bergman–Weil representation becomes identical with Cauchy's integral formula.
, then the Bergman–Weil representation becomes identical with Cauchy's integral formula.
An important property of the Bergman–Weil representation is that its kernel is holomorphic in  . Accordingly, if the holomorphic function
. Accordingly, if the holomorphic function  is replaced by an arbitrary function which is integrable over
is replaced by an arbitrary function which is integrable over 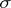 , then the right-hand side of the Weil representation gives a function which is holomorphic everywhere in
, then the right-hand side of the Weil representation gives a function which is holomorphic everywhere in 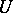 and almost-everywhere in
and almost-everywhere in 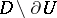 ; such functions are called integrals of Bergman–Weil type. If
; such functions are called integrals of Bergman–Weil type. If  is holomorphic in
is holomorphic in 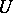 and continuous on
and continuous on  , then its integral of Bergman–Weil type is zero almost-everywhere on
, then its integral of Bergman–Weil type is zero almost-everywhere on  .
.
Bergman–Weil representations in a Weil domain 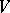 yield, after the substitution
yield, after the substitution
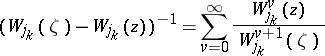 |
the Weil decomposition
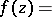 |
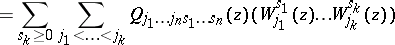 |
into a series of functions, holomorphic in  , and this series is uniformly convergent on compact subsets of
, and this series is uniformly convergent on compact subsets of 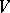 .
.
References
| [1] | S.B. Bergman, Mat. Sb. , 1 (43) (1936) pp. 242–257 |
| [2] | A. Weil, "L'intégrale de Cauchy et les fonctions de plusieurs variables" Math. Ann. , 111 (1935) pp. 178–182 |
| [3] | V.S. Vladimirov, "Methods of the theory of functions of several complex variables" , M.I.T. (1966) (Translated from Russian) |
Comments
References
| [a1] | G.M. [G.M. Khenkin] Henkin, J. Leiterer, "Theory of functions on complex manifolds" , Birkhäuser (1983) |
Bergman-Weil representation. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Bergman-Weil_representation&oldid=18015