Berger inequality
From Encyclopedia of Mathematics
For a compact Riemannian manifold  , let
, let
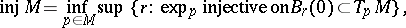 |
where  is the ball around
is the ball around  with radius
with radius  , be the injectivity radius, and set
, be the injectivity radius, and set  . Then the inequality
. Then the inequality
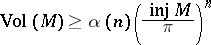 |
holds, with equality if and only if  is isometric to the standard sphere with diameter
is isometric to the standard sphere with diameter  .
.
This inequality relies on the Kazdan inequality applied to the Jacobi equation 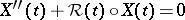 for operators
for operators 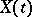 on
on  for a unit vector
for a unit vector 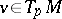 . Here,
. Here,  is the curvature operator,
is the curvature operator, 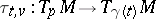 is the parallel transport along the geodesic ray
is the parallel transport along the geodesic ray 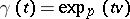 , and
, and 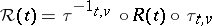 is the parallel translated curvature operator on
is the parallel translated curvature operator on 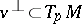 .
.
References
| [a1] | M. Berger, "Une borne inférieure pour le volume d'une variété riemannienes en fonction du rayon d'injectivité" Ann. Inst. Fourier (Grenoble) , 30 (1980) pp. 259–265 |
| [a2] | I. Chavel, "Riemannian geometry: A modern introduction" , Cambridge Univ. Press (1995) |
How to Cite This Entry:
Berger inequality. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Berger_inequality&oldid=15922
Berger inequality. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Berger_inequality&oldid=15922
This article was adapted from an original article by H. Kaul (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article