Benjamin-Bona-Mahony equation
BBM equation, regularized long wave equation
The model equation
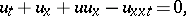 | (a1) |
where  and the subscripts denote partial derivatives with respect to time
and the subscripts denote partial derivatives with respect to time 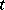 and the position coordinate
and the position coordinate  . The Benjamin–Bona–Mahony equation serves as an approximate model in studying the dynamics of small-amplitude surface water waves propagating unidirectionally, while suffering non-linear and dispersive effects. (a1) was introduced in [a5] as an alternative of the famous Korteweg–de Vries equation
. The Benjamin–Bona–Mahony equation serves as an approximate model in studying the dynamics of small-amplitude surface water waves propagating unidirectionally, while suffering non-linear and dispersive effects. (a1) was introduced in [a5] as an alternative of the famous Korteweg–de Vries equation
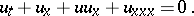 | (a2) |
Unlike the Korteweg–de Vries equation, the Benjamin–Bona–Mahony equation is not integrable by the inverse scattering method [a10], [a12]. As indicated by several numerical experiments, (a1) has no multi-soliton solutions. It has been proved by A.C. Bryan and A.E.G. Stuart [a8] that (a1) has no analytic two-soliton solution. The equation has three independent invariants (conservation laws):
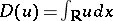 ;
;
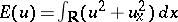 ; and
; and
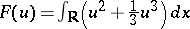 . These quantities are time-independent during the time evolution of the solution
. These quantities are time-independent during the time evolution of the solution  . The correctness of the initial value problem
. The correctness of the initial value problem 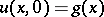 (the Cauchy problem) for (a1) in Sobolev spaces
(the Cauchy problem) for (a1) in Sobolev spaces 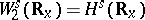 ,
, 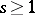 (cf. also Sobolev space), was investigated in [a5].
(cf. also Sobolev space), was investigated in [a5].
Equation (a1) has a solitary wave solution 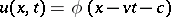 , where
, where 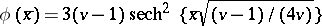 (cf. also Soliton), provided that the wave velocity
(cf. also Soliton), provided that the wave velocity  satisfies
satisfies  . The non-linear stability of the wave
. The non-linear stability of the wave 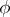 with respect to the pseudo-metric
with respect to the pseudo-metric 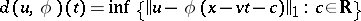 was established in [a3] and [a7] by a clever modification of Lyapunov's direct method in combination with a spectral decomposition technique. Here,
was established in [a3] and [a7] by a clever modification of Lyapunov's direct method in combination with a spectral decomposition technique. Here, 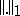 is the norm in the Sobolev space
is the norm in the Sobolev space 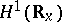 . This means that the form of the solitary wave is stable under small perturbations in the form of the initial wave.
. This means that the form of the solitary wave is stable under small perturbations in the form of the initial wave.
Generalizations.
The generalized Benjamin–Bona–Mahony equation is an equation of the form
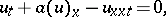 | (a3) |
where 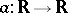 is a differentiable function. (a3) allows two types of solitary waves: kink-shaped and bell-shaped ones. Depending on the concrete form of the non-linearity, these solitary waves can be stable or unstable with respect to the metric
is a differentiable function. (a3) allows two types of solitary waves: kink-shaped and bell-shaped ones. Depending on the concrete form of the non-linearity, these solitary waves can be stable or unstable with respect to the metric 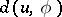 . For more concrete results concerning (a3), see [a11], Chap. 4. The generalized Benjamin–Bona–Mahony equation in higher dimensions reads
. For more concrete results concerning (a3), see [a11], Chap. 4. The generalized Benjamin–Bona–Mahony equation in higher dimensions reads
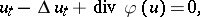 | (a4) |
where 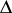 is the Laplace operator in
is the Laplace operator in  and
and 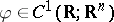 . The uniqueness and global existence of a solution in Sobolev spaces to the initial boundary value problem for (a4) in
. The uniqueness and global existence of a solution in Sobolev spaces to the initial boundary value problem for (a4) in 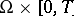 , with Dirichlet (or more general) boundary conditions, was proved in [a2], [a9]. Here,
, with Dirichlet (or more general) boundary conditions, was proved in [a2], [a9]. Here,  is a bounded domain with smooth boundary. The Cauchy problem for (a4) is studied in [a1].
is a bounded domain with smooth boundary. The Cauchy problem for (a4) is studied in [a1].
Non-local generalizations of the Benjamin–Bona–Mahony equation can be obtained after one writes (a1) in the form
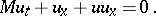 |
Here, 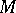 is a pseudo-differential operator (in fact, a Fourier multiplier operator), acting as
is a pseudo-differential operator (in fact, a Fourier multiplier operator), acting as 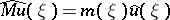 , where
, where  denotes the Fourier transform in the space variable. For the original Benjamin–Bona–Mahony equation one has
denotes the Fourier transform in the space variable. For the original Benjamin–Bona–Mahony equation one has 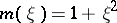 . In general, one takes for
. In general, one takes for 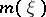 a positive even function such that its negative power
a positive even function such that its negative power 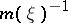 is monotone decreasing on
is monotone decreasing on 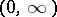 and belongs to
and belongs to 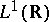 . See [a4], [a5] and the references therein for more details.
. See [a4], [a5] and the references therein for more details.
The variable-coefficient Benjamin–Bona–Mahony equation
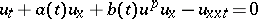 |
describes the propagation of long weakly non-linear water waves in a channel of variable depth. This equation was studied in [a6].
References
| [a1] | J. Avrin, "The generalized Benjamin–Bona–Mahony equation in 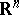 with singular initial data" Nonlin. Anal. Th. Meth. Appl. , 11 (1987) pp. 139–147 with singular initial data" Nonlin. Anal. Th. Meth. Appl. , 11 (1987) pp. 139–147 |
| [a2] | J. Avrin, J.A. Goldstein, "Global existence for the Benjamin–Bona–Mahony equation in arbitrary dimensions" Nonlin. Anal. Th. Meth. Appl. , 9 (1985) pp. 861–865 |
| [a3] | T.B. Benjamin, "The stability of solitary waves" Proc. Royal Soc. London A , 328 (1972) pp. 153–183 |
| [a4] | T.B. Benjamin, "Lectures on nonlinear wave motion" A.C. Newell (ed.) , Nonlinear Wave Motion , Lectures in Applied Math. , 15 , Amer. Math. Soc. (1974) pp. 3–47 |
| [a5] | T.B. Benjamin, J.L. Bona, J.J. Mahony, "Model equations for long waves in nonlinear dispersive systems" Philos. Trans. Royal Soc. London A , 272 (1972) pp. 47–78 |
| [a6] | V. Bisognin, G. Perla Menzala, "Asymptotic behaviour of nonlinear dispersive models with variable coefficients" Ann. Mat. Pura Appl. , 168 (1995) pp. 219–235 |
| [a7] | J.L. Bona, "On the stability theory of solitary waves" Proc. Royal Soc. London A , 344 (1975) pp. 363–374 |
| [a8] | A.C. Bryan, A.E.G. Stuart, "Solitons and the regularized long wave equation: a nonexistence theorem" Chaos, Solitons, Fractals , 7 (1996) pp. 1881–1886 |
| [a9] | B. Calvert, "The equation 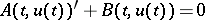 " Math. Proc. Cambridge Philos. Soc. , 79 (1976) pp. 545–561 " Math. Proc. Cambridge Philos. Soc. , 79 (1976) pp. 545–561 |
| [a10] | C.S. Gardner, J.M. Greene, M.D. Kruskal, R.M. Miura, "Method for solving the Korteweg–de Vries equation" Phys. Rev. Lett. , 19 (1967) pp. 1095–1097 |
| [a11] | I.D. Iliev, E. Khristov, K.P. Kirchev, "Spectral methods in soliton equations" , Pitman Monographs and Surveys Pure Appl. Math. , 73 , Longman (1994) |
| [a12] | P.D. Lax, "Integrals of nonlinear equations of evolution and solitary waves" Commun. Pure Appl. Math. , 21 (1968) pp. 467–490 |
Benjamin-Bona-Mahony equation. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Benjamin-Bona-Mahony_equation&oldid=15681