Difference between revisions of "Bellman-Harris process"
(Importing text file) |
(category, MSC) |
||
| Line 1: | Line 1: | ||
| + | [[Category:Branching processes]] | ||
| + | |||
| + | {{User:Rehmann/sandbox/MSC|60J80|}} | ||
| + | |||
A special case of an age-dependent branching process (cf. [[Branching process, age-dependent|Branching process, age-dependent]]). It was first studied by R. Bellman and T.E. Harris [[#References|[1]]]. In the Bellman–Harris process it is assumed that particles live, independently of each other, for random periods of time, and produce a random number of new particles at the end of their life time. If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b015/b015470/b0154701.png" /> is the distribution function of the life times of the individual particles, if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b015/b015470/b0154702.png" /> is the generating function of the number of direct descendants of one particle, and if at time <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b015/b015470/b0154703.png" /> the age of the particle was zero, then the generating function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b015/b015470/b0154704.png" /> of the number of particles <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b015/b015470/b0154705.png" /> satisfies the non-linear integral equation | A special case of an age-dependent branching process (cf. [[Branching process, age-dependent|Branching process, age-dependent]]). It was first studied by R. Bellman and T.E. Harris [[#References|[1]]]. In the Bellman–Harris process it is assumed that particles live, independently of each other, for random periods of time, and produce a random number of new particles at the end of their life time. If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b015/b015470/b0154701.png" /> is the distribution function of the life times of the individual particles, if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b015/b015470/b0154702.png" /> is the generating function of the number of direct descendants of one particle, and if at time <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b015/b015470/b0154703.png" /> the age of the particle was zero, then the generating function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b015/b015470/b0154704.png" /> of the number of particles <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b015/b015470/b0154705.png" /> satisfies the non-linear integral equation | ||
Revision as of 18:49, 11 January 2012
[ 2010 Mathematics Subject Classification MSN: 60J80 | MSCwiki: 60J80 ]
A special case of an age-dependent branching process (cf. Branching process, age-dependent). It was first studied by R. Bellman and T.E. Harris [1]. In the Bellman–Harris process it is assumed that particles live, independently of each other, for random periods of time, and produce a random number of new particles at the end of their life time. If 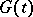 is the distribution function of the life times of the individual particles, if
is the distribution function of the life times of the individual particles, if 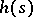 is the generating function of the number of direct descendants of one particle, and if at time
is the generating function of the number of direct descendants of one particle, and if at time 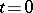 the age of the particle was zero, then the generating function
the age of the particle was zero, then the generating function 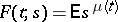 of the number of particles
of the number of particles 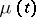 satisfies the non-linear integral equation
satisfies the non-linear integral equation
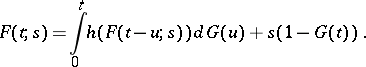 |
If
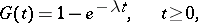 |
the Bellman–Harris process is a Markov branching process with continuous time.
References
| [1] | R. Bellman, T.E. Harris, "On the theory of age-dependent stochastic branching processes" Proc. Nat. Acad. Sci. USA , 34 (1948) pp. 601–604 |
Bellman-Harris process. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Bellman-Harris_process&oldid=14293