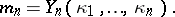The printable version is no longer supported and may have rendering errors. Please update your browser bookmarks and please use the default browser print function instead.
The Bell polynomials (studied extensively by E.T. Bell [a2]) arise naturally from differentiating a composite function  times, but in this context they predate Bell since they are implicit in the work of F. Faà di Bruno [a4]. Accounts of Faà di Bruno's formula, however, often fail to mention any connection with Bell polynomials. The polynomials also occur in other places without being referred to by name; in [a1] (Table 24.2), for example, the numbers
times, but in this context they predate Bell since they are implicit in the work of F. Faà di Bruno [a4]. Accounts of Faà di Bruno's formula, however, often fail to mention any connection with Bell polynomials. The polynomials also occur in other places without being referred to by name; in [a1] (Table 24.2), for example, the numbers  are coefficients of partial Bell polynomials, but are not identified as such.
are coefficients of partial Bell polynomials, but are not identified as such.
Suppose that  and let
and let
then by repeated application of the chain rule:
In general,
 | (a1) |
where  is a homogeneous polynomial of degree
is a homogeneous polynomial of degree 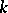 and weight
and weight  in the
in the 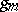 , known as a (partial) Bell polynomial (see [a3] for a table for
, known as a (partial) Bell polynomial (see [a3] for a table for  ); it has integral coefficients. Because of the homogeneity, for fixed
); it has integral coefficients. Because of the homogeneity, for fixed  all
all 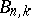 (
( ) can be determined uniquely even if the
) can be determined uniquely even if the 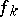 are omitted. Hence the (complete) Bell polynomial
are omitted. Hence the (complete) Bell polynomial  is usually defined for
is usually defined for 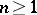 by
by
In [a7], however, the term Bell polynomial is used for
so the 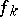 are included in the definition.
are included in the definition.
The following definitions are also made:  ,
, 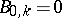 (
(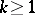 ),
),  .
.
Although the  were introduced as derivatives, the Bell polynomials themselves, considered purely as polynomials in the variables
were introduced as derivatives, the Bell polynomials themselves, considered purely as polynomials in the variables 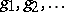 are independent of the initial functions
are independent of the initial functions 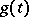 and
and  . Hence information can be deduced from special choices such as
. Hence information can be deduced from special choices such as  , which gives
, which gives
An alternative approach which gives the same polynomials 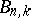 is adopted in [a3], where they are defined as coefficients in the expansion of the two-variable generating function
is adopted in [a3], where they are defined as coefficients in the expansion of the two-variable generating function
This approach obviates the earlier assumption that the  are derivatives.
are derivatives.
The generating function for the complete polynomials is
Explicit formulas are known for Bell polynomials and they are examples of partition polynomials (multivariable polynomials which can be expressed as a sum of monomials, where the sum is over a set of partitions of  ; cf. also Partition). The partial polynomial
; cf. also Partition). The partial polynomial
where the sum is over all partitions of  into exactly
into exactly 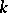 non-negative parts, i.e., over all solutions in non-negative integers
non-negative parts, i.e., over all solutions in non-negative integers 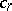 of the two equations
of the two equations
Since, for each fixed 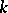 , there can be no parts of size greater than
, there can be no parts of size greater than  , the formula is often stated in the simpler looking, but equivalent, form (where necessarily
, the formula is often stated in the simpler looking, but equivalent, form (where necessarily  ):
):
 | (a2) |
where the sum is over all solutions in non-negative integers of the equations
The complete polynomial
where the sum is over all partitions of  into arbitrarily many non-negative parts, i.e., over all non-negative integer solutions of the single equation
into arbitrarily many non-negative parts, i.e., over all non-negative integer solutions of the single equation
There are many recurrence relations for Bell polynomials, as well as formulas connecting them with other special polynomials and numbers; the following is a small selection, and others may be found in [a3], [a7], [a8].
where  and
and 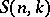 are Stirling numbers of the first and second kinds (cf. Combinatorial analysis), respectively;
are Stirling numbers of the first and second kinds (cf. Combinatorial analysis), respectively;
where  is the Lah number;
is the Lah number;
where  are the Bell numbers.
are the Bell numbers.
Combining equations (a1) and (a2) gives Faà di Bruno's formula for the  th derivative of a composite function:
th derivative of a composite function:
summed over all solutions in non-negative integers of
(For a generalization to functions of several variables, see [a5].)
The formula can be used, in particular, to express functions of power series as power series. If
and
then
and Faà di Bruno's formula can be used to find  . For example, if
. For example, if 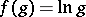 , then
, then
Hence, applying the formula and evaluating the result at  gives
gives
 | (a3) |
Thus, provided that  ,
,
A special case of (a3) is used [a6] to express the cumulants (semi-invariants, cf. Semi-invariant) 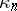 of a probability distribution
of a probability distribution  in terms of its moments (cf. Moment)
in terms of its moments (cf. Moment)
The probability generating function of the distribution is
and it is easy to show that
The cumulants 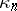 (
(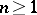 ) and their exponential generating function
) and their exponential generating function 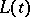 are defined in terms of
are defined in terms of  by
by
Since 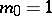 , it follows from (a3) that
, it follows from (a3) that
Similarly, starting from
and applying Faà di Bruno's formula with 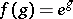 and
and 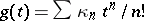 (and noting that in this case
(and noting that in this case  for all
for all 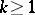 ), the inverse relation expressing moments in terms of cumulants reduces to
), the inverse relation expressing moments in terms of cumulants reduces to
References
| [a1] | M. Abramowitz, I. Stegun, "Handbook of mathematical functions" , Dover, reprint (1965) |
| [a2] | E.T. Bell, "Exponential polynomials" Ann. of Math. , 35 (1934) pp. 258–277 |
| [a3] | L. Comtet, "Advanced combinatorics" , Reidel (1974) |
| [a4] | F. Faà di Bruno, "Note sur une nouvelle formule du calcul différentiel" Quart. J. Math. , 1 (1855) pp. 359–360 |
| [a5] | I.J. Good, "The multivariate saddlepoint method and chi-squared for the multinomial distribution" Ann. Math. Stat. , 32 (1961) pp. 535–548 |
| [a6] | E. Lukács, "Applications of Faà di Bruno's formula in mathematical statistics" Amer. Math. Monthly , 62 (1955) pp. 340–348 |
| [a7] | J. Riordan, "Combinatorial identities" , Wiley (1968) |
| [a8] | S. Roman, "The umbral calculus" , Acad. Press (1984) |
 times, but in this context they predate Bell since they are implicit in the work of F. Faà di Bruno [a4]. Accounts of Faà di Bruno's formula, however, often fail to mention any connection with Bell polynomials. The polynomials also occur in other places without being referred to by name; in [a1] (Table 24.2), for example, the numbers
times, but in this context they predate Bell since they are implicit in the work of F. Faà di Bruno [a4]. Accounts of Faà di Bruno's formula, however, often fail to mention any connection with Bell polynomials. The polynomials also occur in other places without being referred to by name; in [a1] (Table 24.2), for example, the numbers  are coefficients of partial Bell polynomials, but are not identified as such.
are coefficients of partial Bell polynomials, but are not identified as such.
 and let
and let
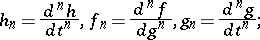
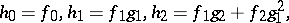
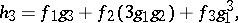
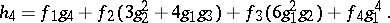

 is a homogeneous polynomial of degree
is a homogeneous polynomial of degree 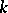 and weight
and weight  in the
in the 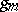 , known as a (partial) Bell polynomial (see [a3] for a table for
, known as a (partial) Bell polynomial (see [a3] for a table for  ); it has integral coefficients. Because of the homogeneity, for fixed
); it has integral coefficients. Because of the homogeneity, for fixed  all
all 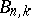 (
( ) can be determined uniquely even if the
) can be determined uniquely even if the 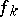 are omitted. Hence the (complete) Bell polynomial
are omitted. Hence the (complete) Bell polynomial  is usually defined for
is usually defined for 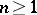 by
by
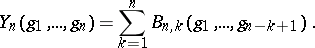
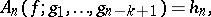
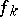 are included in the definition.
are included in the definition.
 ,
, 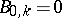 (
(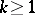 ),
),  .
.
 were introduced as derivatives, the Bell polynomials themselves, considered purely as polynomials in the variables
were introduced as derivatives, the Bell polynomials themselves, considered purely as polynomials in the variables 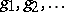 are independent of the initial functions
are independent of the initial functions 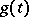 and
and  . Hence information can be deduced from special choices such as
. Hence information can be deduced from special choices such as  , which gives
, which gives
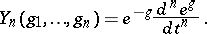
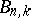 is adopted in [a3], where they are defined as coefficients in the expansion of the two-variable generating function
is adopted in [a3], where they are defined as coefficients in the expansion of the two-variable generating function
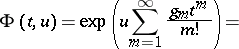
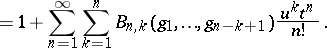
 are derivatives.
are derivatives.
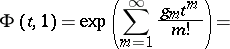
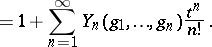
 ; cf. also Partition). The partial polynomial
; cf. also Partition). The partial polynomial
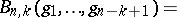
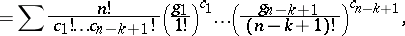
 into exactly
into exactly 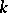 non-negative parts, i.e., over all solutions in non-negative integers
non-negative parts, i.e., over all solutions in non-negative integers 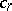 of the two equations
of the two equations
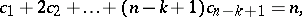
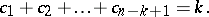
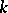 , there can be no parts of size greater than
, there can be no parts of size greater than  , the formula is often stated in the simpler looking, but equivalent, form (where necessarily
, the formula is often stated in the simpler looking, but equivalent, form (where necessarily  ):
):

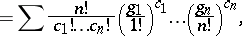
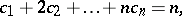
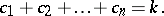
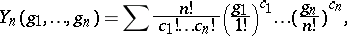
 into arbitrarily many non-negative parts, i.e., over all non-negative integer solutions of the single equation
into arbitrarily many non-negative parts, i.e., over all non-negative integer solutions of the single equation
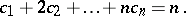
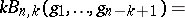
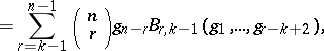
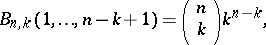
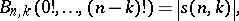
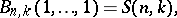
 and
and 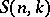 are Stirling numbers of the first and second kinds (cf. Combinatorial analysis), respectively;
are Stirling numbers of the first and second kinds (cf. Combinatorial analysis), respectively;
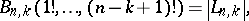
 is the Lah number;
is the Lah number;
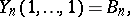
 are the Bell numbers.
are the Bell numbers.
 th derivative of a composite function:
th derivative of a composite function:
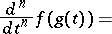
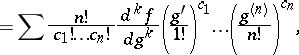
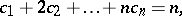
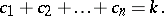
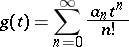
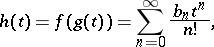
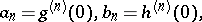
 . For example, if
. For example, if 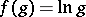 , then
, then
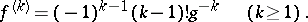
 gives
gives

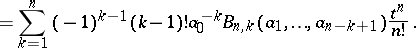
 ,
,
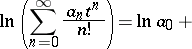
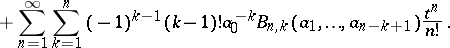
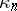 of a probability distribution
of a probability distribution  in terms of its moments (cf. Moment)
in terms of its moments (cf. Moment)
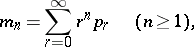
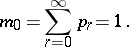
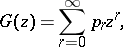
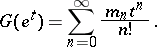
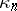 (
(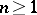 ) and their exponential generating function
) and their exponential generating function 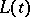 are defined in terms of
are defined in terms of  by
by
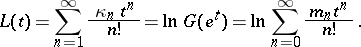
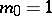 , it follows from (a3) that
, it follows from (a3) that
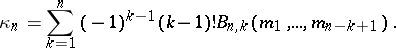
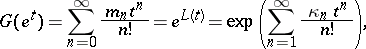
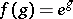 and
and 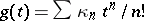 (and noting that in this case
(and noting that in this case  for all
for all 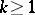 ), the inverse relation expressing moments in terms of cumulants reduces to
), the inverse relation expressing moments in terms of cumulants reduces to