Beckman-Quarles-type theorems
A fundamental theorem in Euclidean geometry is the following result of F.S. Beckman and D.A. Quarles [a1]. Let 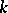 be a fixed positive real number and let
be a fixed positive real number and let 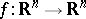 (
(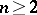 ) be a mapping satisfying
) be a mapping satisfying 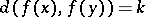 for all
for all 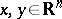 with
with 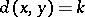 . (Here,
. (Here, 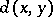 denotes the Euclidean distance
denotes the Euclidean distance
 |
of 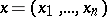 and
and 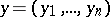 in
in 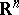 .) The mapping
.) The mapping 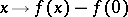 is then in
is then in 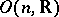 .
.
It should be emphasized that no regularity assumption (like differentiability or continuity) is required in the theorem. For an analogue in hyperbolic geometry, see [a4] and [a5].
A distance space is a set 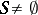 , a set
, a set 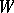 and a mapping
and a mapping  . The element
. The element 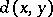 is called the distance of
is called the distance of  and
and 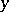 (in this order). Beckman–Quarles-type theorems for distance spaces are, up to generalizations, statements claiming that a mapping
(in this order). Beckman–Quarles-type theorems for distance spaces are, up to generalizations, statements claiming that a mapping 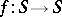 preserves all occurring distances
preserves all occurring distances 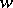 if it preserves one single distance. Beckman–Quarles-type theorems belong to a class of statements called characterizations of geometrical mappings under mild hypotheses.
if it preserves one single distance. Beckman–Quarles-type theorems belong to a class of statements called characterizations of geometrical mappings under mild hypotheses.
Let 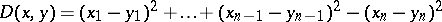 , for
, for 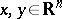 . Let
. Let  be a fixed real number and let
be a fixed real number and let 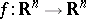 (
(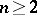 ) be a mapping satisfying
) be a mapping satisfying 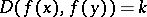 for all
for all 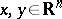 with
with  . Then
. Then 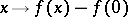 is a Lorentz transformation of
is a Lorentz transformation of 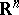 . For
. For  and
and 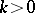 , this was proved by J. Lester; for
, this was proved by J. Lester; for 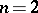 and for
and for 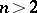 and
and 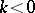 this was proved by W. Benz (see [a2] for all these results). The proofs are different for the three cases, and no common proof is known (1996).
this was proved by W. Benz (see [a2] for all these results). The proofs are different for the three cases, and no common proof is known (1996).
Let 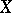 and
and 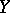 be normed real vector spaces such that
be normed real vector spaces such that 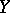 is strictly convex and the dimension of
is strictly convex and the dimension of 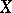 is at least
is at least  (cf. also Vector space; Convex set). Let
(cf. also Vector space; Convex set). Let 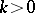 be a fixed real number and
be a fixed real number and 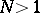 a fixed integer. Suppose that
a fixed integer. Suppose that 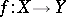 is a mapping satisfying
is a mapping satisfying
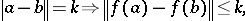 |
 |
for all 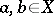 . Then
. Then 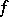 is an isometric operator, and hence an affine transformation (the Benz–Berens theorem, [a2]). If
is an isometric operator, and hence an affine transformation (the Benz–Berens theorem, [a2]). If 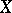 and
and 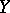 are, in addition, pre-Hilbert spaces (cf. Pre-Hilbert space), then
are, in addition, pre-Hilbert spaces (cf. Pre-Hilbert space), then 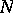 may be replaced by any real number greater than
may be replaced by any real number greater than 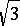 (Radó–Andreascu–Valcán theorem).
(Radó–Andreascu–Valcán theorem).
There are generalizations for finite planes [a9], rational or constructible curves (B. Farrahi), non-Euclidean spaces [a11], and planes over fields [a10]. F. Radó [a8] has proved the following theorem. Let 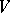 be a non-singular metric vector space of dimension
be a non-singular metric vector space of dimension 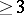 over
over 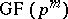 ,
, 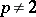 ,
, 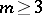 , and let
, and let  be a fixed element of
be a fixed element of 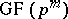 . If
. If 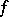 is a bijection of
is a bijection of 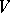 preserving distance
preserving distance 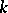 , then
, then 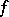 is a semi-affine mapping if
is a semi-affine mapping if  .
.
Let  ,
, 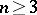 , be a mapping satisfying
, be a mapping satisfying
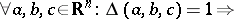 |
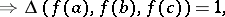 |
where 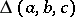 denotes the area of the triangle with vertices
denotes the area of the triangle with vertices  . Then
. Then 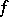 is a Euclidean motion, i.e.,
is a Euclidean motion, i.e., 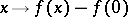 is in
is in 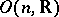 (Lester's theorem), [a3]. For
(Lester's theorem), [a3]. For 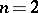 the equi-affine mappings are characterized similarly.
the equi-affine mappings are characterized similarly.
Let 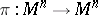 be a mapping of the set
be a mapping of the set 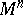 of lines in
of lines in  ,
, 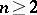 , into itself such that whenever
, into itself such that whenever  are the lines making up the sides of a triangle of area
are the lines making up the sides of a triangle of area 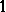 , then
, then 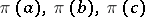 are also the sides of a triangle of area
are also the sides of a triangle of area 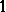 . Then
. Then 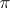 is induced by a Euclidean motion of
is induced by a Euclidean motion of 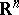 for
for 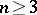 and by an equi-affine mapping if
and by an equi-affine mapping if 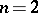 (the Wen-ling Huang theorem, [a3]).
(the Wen-ling Huang theorem, [a3]).
Let 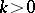 be a fixed real number and
be a fixed real number and 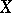 a normed real vector space of dimension
a normed real vector space of dimension 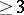 . Let
. Let 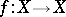 be a function satisfying
be a function satisfying
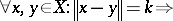 |
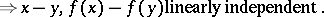 |
Then there are elements 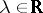 and
and 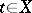 such that
such that 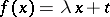 for all
for all 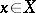 . This theorem was proved by Benz [a2] and, anew, by D. Laugwitz [a6].
. This theorem was proved by Benz [a2] and, anew, by D. Laugwitz [a6].
General references for this area are [a2], [a3] and [a7].
References
| [a1] | F.S. Beckman, D.A. Quarles, jr., "On isometries of Euclidean spaces" Proc. Amer. Math. Soc. , 4 (1953) pp. 810–815 |
| [a2] | W. benz, "Geometrische Transformationen (unter besonderer Berücksichtingung der Lorentztransformationen)" , BI Wissenschaftsverlag (1992) |
| [a3] | W. Benz, "Real geometries" , BI Wissenschaftsverlag (1994) |
| [a4] | B. Farrahi, "A characerization of isometries of absolute planes" Resultate Math. , 4 (1981) pp. 34–38 |
| [a5] | A.V. Kuz'minykh, "Mappings preserving a unit distance" Sibirsk. Mat. Zh. , 20 (1979) pp. 597–602 (In Russian) |
| [a6] | D. Laugwitz, "Regular hexagons in normed spaces and a theorem of Walter Benz" Aequat. Math. , 45 (1993) pp. 163–166 |
| [a7] | J. Lester, "Distance preserving transformations" F. Buekenhout (ed.) , Handbook of Incidence geometry , Elsevier (1995) |
| [a8] | F. Radó, "On mappings of the Galois space" Israel J. Math. , 53 (1986) pp. 217–230 |
| [a9] | H.-J. Samaga, "Zur Kennzeichnung von Lorentztransformationen in endlichen Ebenen" J. Geom. , 18 (1982) pp. 169–184 |
| [a10] | H. Schaeffer, "Der Satz von Benz–Radó" Aequat. Math. , 31 (1986) pp. 300–309 |
| [a11] | E.M. Schröder, "Zur Kennzeichnung distanztreuer Abbildungen in nichteuklidischen Räumen" J. Geom. , 15 (1980) pp. 108–118 |
Beckman-Quarles-type theorems. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Beckman-Quarles-type_theorems&oldid=22075