Bayes formula
A formula with which it is possible to compute a posteriori probabilities of events (or of hypotheses) from a priori probabilities. Let  be a complete group of incompatible events:
be a complete group of incompatible events:  ,
, 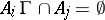 if
if  . Then the a posteriori probability
. Then the a posteriori probability  of event
of event  if given that event
if given that event  with
with  has already occurred may be found by Bayes' formula:
has already occurred may be found by Bayes' formula:
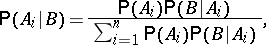 | (*) |
where  is the a priori probability of
is the a priori probability of  ,
,  is the conditional probability of event
is the conditional probability of event 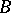 occurring given event
occurring given event 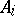 (with
(with 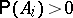 ) has taken place. The formula was demonstrated by T. Bayes in 1763.
) has taken place. The formula was demonstrated by T. Bayes in 1763.
Formula (*) is a special case of the following abstract variant of Bayes' formula. Let 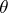 and
and 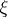 be random elements with values in measurable spaces
be random elements with values in measurable spaces  and
and  and let
and let  . Put, for any set
. Put, for any set  ,
,
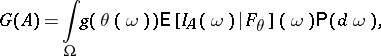 |
where  and
and 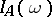 is the indicator of the set
is the indicator of the set 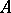 . Then the measure
. Then the measure 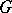 is absolutely continuous with respect to the measure
is absolutely continuous with respect to the measure  (
( ) and
) and  , where
, where  is the Radon–Nikodým derivative of
is the Radon–Nikodým derivative of  with respect to
with respect to  .
.
References
| [1] | A.N. Kolmogorov, "Foundations of the theory of probability" , Chelsea, reprint (1950) (Translated from Russian) |
Comments
References
| [a1] | R.S. Liptser, A.N. Shiryaev, "Statistics of random processes" , 1 , Springer (1977) pp. Section 7.9 (Translated from Russian) |
Bayes formula. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Bayes_formula&oldid=16075