Bateman function

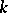-function

The function

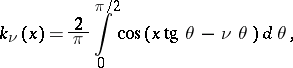(1)

where and are real numbers. The function was defined by H. Bateman [1]. The Bateman function may be expressed in the form of a confluent hypergeometric function of the second kind :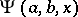

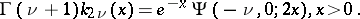(2)

The relation (2) is conveniently taken as the definition of the Bateman function in the complex plane with the cut 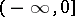. The following relations are valid: for case (1)

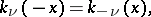for case (2)

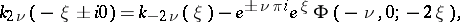where 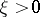, and 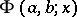is a confluent hypergeometric function of the first kind.

References

[1]	H. Bateman, "The 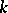-function, a particular case of the confluent hypergeometric function" Trans. Amer. Math. Soc. , 33 (1931) pp. 817–831
[2]	H. Bateman (ed.) A. Erdélyi (ed.) , Higher transcendental functions , 1. The gamma function. The hypergeometric functions. Legendre functions , McGraw-Hill (1953)