Basis
of a set 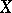
A minimal subset 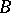 that generates it. Generation here means that by application of operations of a certain class
that generates it. Generation here means that by application of operations of a certain class  to elements
to elements 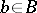 it is possible to obtain any element
it is possible to obtain any element 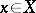 . This concept is related to the concept of dependence: By means of operations from
. This concept is related to the concept of dependence: By means of operations from  the elements of
the elements of 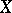 become dependent on the elements of
become dependent on the elements of 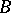 . Minimality means that no proper subset
. Minimality means that no proper subset 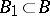 generates
generates 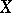 . In a certain sense this property causes the elements of
. In a certain sense this property causes the elements of 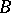 to be independent: None of the elements
to be independent: None of the elements 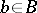 is generated by the other elements of
is generated by the other elements of 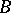 . For instance, the set of all natural numbers
. For instance, the set of all natural numbers 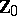 has the unique element 0 as basis and is generated from it by the operation of immediate succession and its iteration. The set of all natural numbers
has the unique element 0 as basis and is generated from it by the operation of immediate succession and its iteration. The set of all natural numbers 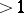 is generated by the operation of multiplication from the basis consisting of all prime numbers. A basis of the algebra of quaternions consists of the four elements
is generated by the operation of multiplication from the basis consisting of all prime numbers. A basis of the algebra of quaternions consists of the four elements 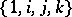 if the generating operations consist of addition and of multiplication by real numbers; if, in addition to these operations, one also includes multiplication of quaternions, the basis will consist of three elements only —
if the generating operations consist of addition and of multiplication by real numbers; if, in addition to these operations, one also includes multiplication of quaternions, the basis will consist of three elements only — 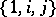 (because
(because 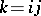 ).
).
A basis of the natural numbers of order 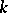 is a subsequence
is a subsequence  of the set
of the set 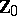 of natural numbers including 0, which, as a result of
of natural numbers including 0, which, as a result of 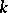 -fold addition to itself (the generating operation) yields all of
-fold addition to itself (the generating operation) yields all of 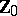 . This means that any natural number
. This means that any natural number  can be represented in the form
can be represented in the form
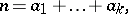 |
where 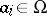 . For example, every natural number is a sum of four squares of natural numbers (Lagrange's theorem), i.e. the sequence of squares is a basis of
. For example, every natural number is a sum of four squares of natural numbers (Lagrange's theorem), i.e. the sequence of squares is a basis of 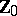 of order 4. In general, the sequence of
of order 4. In general, the sequence of 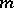 -th powers of natural numbers is a basis of
-th powers of natural numbers is a basis of 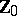 (Hilbert's theorem), the order of which has been estimated by the Vinogradov method. The concept of a basis of
(Hilbert's theorem), the order of which has been estimated by the Vinogradov method. The concept of a basis of 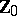 has been generalized to the case of arbitrary sequences of numbers, i.e. functions on
has been generalized to the case of arbitrary sequences of numbers, i.e. functions on 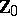 .
.
A set 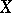 always contains a generating set (in the trivial case:
always contains a generating set (in the trivial case: 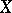 generates
generates 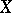 ), but minimality may prove to be principally impossible (such a situation is typical of classes
), but minimality may prove to be principally impossible (such a situation is typical of classes  containing infinite-place operations, in particular in topological structures, lattices, etc.). For this reason the minimality condition is replaced by a weaker requirement: A basis is a generating set of minimal cardinality. In this context a basis
containing infinite-place operations, in particular in topological structures, lattices, etc.). For this reason the minimality condition is replaced by a weaker requirement: A basis is a generating set of minimal cardinality. In this context a basis 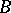 is defined as a parametrized set (or population), i.e. as a function
is defined as a parametrized set (or population), i.e. as a function 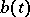 on a set of indices
on a set of indices 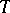 with values in
with values in 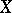 , such that
, such that 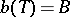 ; the cardinality of
; the cardinality of 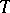 is sometimes called as the dimension (or rank) of the basis of
is sometimes called as the dimension (or rank) of the basis of 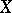 . For example, a countable everywhere-dense set
. For example, a countable everywhere-dense set 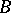 in a separable topological space
in a separable topological space 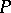 may be considered as a basis for it;
may be considered as a basis for it; 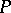 is generated from
is generated from 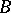 by the closure operation (which, incidentally, is related to generation in more general cases as well, see below).
by the closure operation (which, incidentally, is related to generation in more general cases as well, see below).
A basis for a topology of a topological space 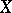 (a base) is a basis
(a base) is a basis 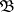 of the set of all open subsets in
of the set of all open subsets in 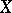 ; the generation is effected by taking unions of elements of
; the generation is effected by taking unions of elements of 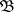 .
.
A basis of a Boolean algebra 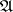 (a dual base of
(a dual base of 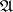 in the sense of Tarski) is a dense set
in the sense of Tarski) is a dense set 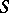 (of minimal cardinality) in
(of minimal cardinality) in 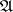 ; the generation of
; the generation of 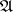 from
from 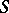 (and hence
(and hence 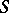 itself) is determined by the condition
itself) is determined by the condition 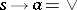 (which is equivalent to
(which is equivalent to 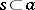 ), where
), where 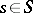 ,
, 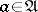 ,
,  is the unit of
is the unit of 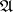 and "" is the operation of implication. One also introduces in an analogous manner a basis for a filter
and "" is the operation of implication. One also introduces in an analogous manner a basis for a filter  as a set
as a set 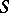 such that for an arbitrary
such that for an arbitrary 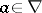 there exists an
there exists an 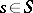 with
with 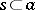 .
.
More special cases of bases of a set 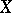 are introduced according to the following procedure. Let
are introduced according to the following procedure. Let 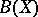 be the Boolean algebra of
be the Boolean algebra of 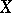 , i.e. the set of all its subsets. A generating operator (or a closure operator)
, i.e. the set of all its subsets. A generating operator (or a closure operator) 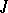 is a mapping of
is a mapping of 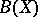 into itself such that if
into itself such that if 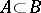 , then
, then 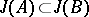 ;
; 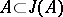 ;
; 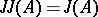 .
.
An element 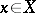 is generated by a set
is generated by a set 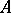 if
if 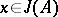 ; in particular,
; in particular, 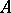 generates
generates 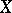 if
if 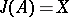 . A minimal set
. A minimal set 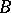 possessing this property is said to be a basis of
possessing this property is said to be a basis of 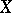 defined by the operator
defined by the operator 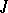 . A generating operator
. A generating operator 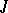 is of finite type if, for arbitrary
is of finite type if, for arbitrary 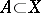 and
and 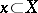 , it follows from
, it follows from 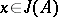 that
that 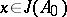 for a certain finite subset
for a certain finite subset 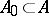 ; a generating operator
; a generating operator 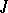 has the property of substitution if, for any
has the property of substitution if, for any 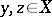 and
and 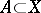 , both
, both  and
and 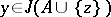 imply that
imply that 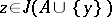 . A generating operator
. A generating operator 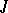 of finite type with the substitution property defines a dependence relation on
of finite type with the substitution property defines a dependence relation on 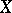 , i.e. a subdivision of
, i.e. a subdivision of 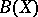 into two classes — dependent and independent sets; a set
into two classes — dependent and independent sets; a set 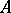 is said to be dependent if
is said to be dependent if 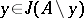 for some
for some 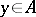 , and is said to be independent if
, and is said to be independent if 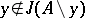 for any
for any 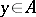 . Therefore,
. Therefore, 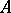 is dependent (independent) if and only if some (arbitrary) non-empty finite subset(s)
is dependent (independent) if and only if some (arbitrary) non-empty finite subset(s) 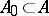 is dependent (are independent).
is dependent (are independent).
For a set 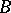 to be a basis of the set
to be a basis of the set 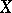 it is necessary and sufficient for
it is necessary and sufficient for 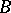 to be an independent generating set for
to be an independent generating set for 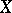 , or else, a maximal independent set in
, or else, a maximal independent set in 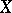 .
.
If 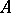 is an arbitrary independent set, and
is an arbitrary independent set, and 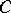 is an
is an 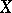 -generating set containing
-generating set containing 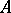 , then there exists a basis
, then there exists a basis 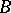 in
in 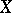 such that
such that 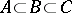 . In particular,
. In particular, 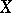 always has a basis, and any two bases of it have the same cardinality.
always has a basis, and any two bases of it have the same cardinality.
In algebraic systems 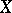 an important role is played by the concept of the so-called free basis
an important role is played by the concept of the so-called free basis 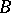 , which is characterized by the following property: Any mapping of
, which is characterized by the following property: Any mapping of 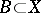 into any algebraic system
into any algebraic system 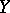 (of the same signature) may be extended to a (unique) (homo)morphism from
(of the same signature) may be extended to a (unique) (homo)morphism from 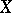 into
into 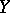 or, which is the same thing, for any (homo)morphism
or, which is the same thing, for any (homo)morphism 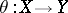 and any set
and any set 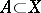 , the generating operators
, the generating operators 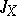 and
and 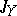 satisfy the condition:
satisfy the condition:
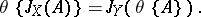 |
An algebraic system with a free basis is said to be free.
A typical example is a basis of a (unitary) module 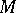 over a ring
over a ring 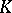 , that is, a free family of elements from
, that is, a free family of elements from 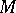 generating
generating 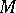 [3]. Here, a family
[3]. Here, a family 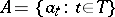 of elements of a
of elements of a 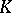 -module
-module 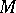 is said to be free if
is said to be free if 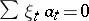 (where
(where 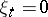 for all except a finite number of indices
for all except a finite number of indices 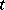 ) implies that
) implies that 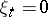 for all
for all 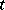 , and the generation is realized by representing the elements
, and the generation is realized by representing the elements  as linear combinations of the elements
as linear combinations of the elements 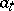 : There exists a set (dependent on
: There exists a set (dependent on  ) of elements
) of elements 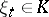 such that
such that 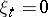 for all except a finite number of indices
for all except a finite number of indices 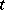 , and such that the decomposition
, and such that the decomposition
 |
is valid (i.e. 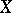 is the linear envelope of
is the linear envelope of 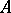 ). In this sense, the basis
). In this sense, the basis 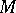 is free basis; the converse proposition is also true. Thus, the set of periods of a doubly-periodic function
is free basis; the converse proposition is also true. Thus, the set of periods of a doubly-periodic function 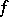 of one complex variable, which is a discrete Abelian group (and hence a module over the ring
of one complex variable, which is a discrete Abelian group (and hence a module over the ring 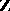 ), has a free basis, called the period basis of
), has a free basis, called the period basis of 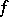 ; it consists of two so-called primitive periods. A period basis of an Abelian function of several complex variables is defined in a similar manner.
; it consists of two so-called primitive periods. A period basis of an Abelian function of several complex variables is defined in a similar manner.
If 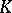 is a skew-field, all bases (in the previous sense) are free. On the contrary, there exist modules without a free basis; these include, for example, the non-principal ideals in an integral domain
is a skew-field, all bases (in the previous sense) are free. On the contrary, there exist modules without a free basis; these include, for example, the non-principal ideals in an integral domain 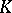 , considered as a
, considered as a 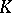 -module.
-module.
A basis of a vector space 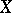 over a field
over a field 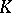 is a (free) basis of the unitary module which underlies
is a (free) basis of the unitary module which underlies 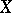 . In a similar manner, a basis of an algebra
. In a similar manner, a basis of an algebra 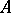 over a field
over a field 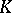 is a basis of the vector space underlying
is a basis of the vector space underlying 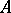 . All bases of a given vector space
. All bases of a given vector space 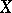 have the same cardinality, which is equal to the cardinality of
have the same cardinality, which is equal to the cardinality of 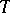 ; the latter is called the algebraic dimension of
; the latter is called the algebraic dimension of 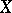 . Each element
. Each element 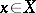 can be represented as a linear combination of basis elements in a unique way. The elements
can be represented as a linear combination of basis elements in a unique way. The elements 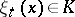 , which are linear functionals on
, which are linear functionals on 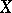 , are called the components (coordinates) of
, are called the components (coordinates) of  in the given basis
in the given basis 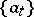 .
.
A set 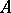 is a basis in
is a basis in 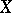 if and only if
if and only if 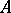 is a maximal (with respect to inclusion) free set in
is a maximal (with respect to inclusion) free set in 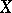 .
.
The mapping
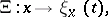 |
where 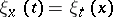 if
if 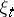 is the value of the
is the value of the 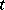 -th component of
-th component of  in the basis
in the basis 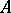 , and 0 otherwise, is called the basis mapping; it is a linear injective mapping of
, and 0 otherwise, is called the basis mapping; it is a linear injective mapping of 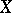 into the space
into the space  of functions on
of functions on 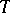 with values in
with values in 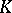 . In this case the image
. In this case the image 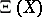 consists of all functions with a finite number of non-zero values (functions of finite support). This interpretation permits one to define a generalized basis of a vector space
consists of all functions with a finite number of non-zero values (functions of finite support). This interpretation permits one to define a generalized basis of a vector space 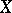 over a field
over a field 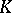 as a bijective linear mapping from it to some subspace
as a bijective linear mapping from it to some subspace 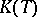 of the space
of the space 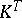 of functions on
of functions on 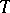 with values in
with values in 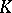 , where
, where 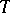 is some suitably chosen set. However, unless additional restrictions (e.g. an order) and additional structures (e.g. a topology) are imposed on
is some suitably chosen set. However, unless additional restrictions (e.g. an order) and additional structures (e.g. a topology) are imposed on 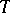 , and corresponding compatible conditions on
, and corresponding compatible conditions on 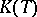 are introduced, the concept of a generalized basis is seldom of use in practice.
are introduced, the concept of a generalized basis is seldom of use in practice.
A basis of a vector space 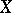 is sometimes called an algebraic basis; in this way it is stressed that there is no connection with additional structures on
is sometimes called an algebraic basis; in this way it is stressed that there is no connection with additional structures on 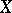 , even if they are compatible with its vector structure.
, even if they are compatible with its vector structure.
A Hamel basis is a basis of the field of real numbers 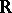 , considered as a vector space over the field of rational numbers. It was introduced by G. Hamel [4] to obtain a discontinuous solution of the functional equation
, considered as a vector space over the field of rational numbers. It was introduced by G. Hamel [4] to obtain a discontinuous solution of the functional equation 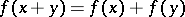 ; the graph of its solution is everywhere dense in the plane
; the graph of its solution is everywhere dense in the plane 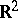 . To each almost-periodic function corresponds some countable Hamel basis
. To each almost-periodic function corresponds some countable Hamel basis 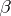 such that each Fourier exponent
such that each Fourier exponent 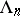 of this function belongs to the linear envelope of
of this function belongs to the linear envelope of 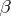 . The elements of
. The elements of 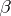 may be so chosen that they belong to a sequence
may be so chosen that they belong to a sequence 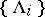 ; the set
; the set 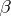 is said to be a basis of the almost-periodic functions. An analogous basis has been constructed in a ring containing a skew-field
is said to be a basis of the almost-periodic functions. An analogous basis has been constructed in a ring containing a skew-field 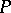 and which has the unit of
and which has the unit of 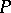 as its own unit. An algebraic basis of an arbitrary vector space is also sometimes referred to as a Hamel basis.
as its own unit. An algebraic basis of an arbitrary vector space is also sometimes referred to as a Hamel basis.
A topological basis (a basis of a topological vector space 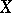 over a field
over a field 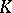 ) is a set
) is a set 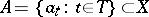 with properties and functions analogous to those of the algebraic basis of the vector space. The concept of a topological basis, which is one of the most important ones in functional analysis, generalizes the concept of an algebraic basis with regard to the topological structure of
with properties and functions analogous to those of the algebraic basis of the vector space. The concept of a topological basis, which is one of the most important ones in functional analysis, generalizes the concept of an algebraic basis with regard to the topological structure of 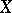 and makes it possible to obtain, for each element
and makes it possible to obtain, for each element 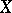 , its decomposition with respect to the basis
, its decomposition with respect to the basis 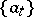 , which is moreover unique, i.e. a representation of
, which is moreover unique, i.e. a representation of  as a limit (in some sense) of linear combinations of elements
as a limit (in some sense) of linear combinations of elements 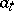 :
:
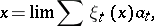 |
where 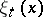 are linear functionals on
are linear functionals on 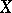 with values in
with values in 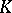 , called the components of
, called the components of  in the basis
in the basis 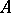 , or the coefficients of the decomposition of
, or the coefficients of the decomposition of  with respect to the basis
with respect to the basis 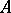 . Clearly, for the decomposition of an arbitrary
. Clearly, for the decomposition of an arbitrary  to exist,
to exist, 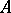 must be a complete set in
must be a complete set in 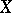 , and for such a decomposition to be unique (i.e. for the zero element of
, and for such a decomposition to be unique (i.e. for the zero element of 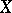 to have all components equal to zero),
to have all components equal to zero), 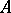 must be a topologically free set in
must be a topologically free set in 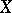 .
.
The sense and the practical significance of a topological basis (which will be simply denoted as a "basis" in what follows) is to establish a bijective linear mapping of 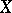 , called the basis mapping,
, called the basis mapping, 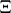 into some (depending on
into some (depending on 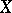 ) space
) space 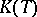 of functions with values in
of functions with values in 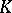 , defined on a (topological) space
, defined on a (topological) space 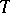 , viz.:
, viz.:
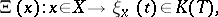 |
where 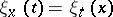 , so that, symbolically,
, so that, symbolically, 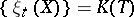 and
and 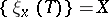 . Owing to its concrete, effective definition, the structure of
. Owing to its concrete, effective definition, the structure of 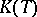 is simpler and more illustrative than that of the abstractly given
is simpler and more illustrative than that of the abstractly given 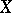 . For instance, an algebraic basis of an infinite-dimensional Banach space is not countable, while in a number of cases, if the concept of a basis is suitably generalized, the cardinality of
. For instance, an algebraic basis of an infinite-dimensional Banach space is not countable, while in a number of cases, if the concept of a basis is suitably generalized, the cardinality of 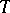 is substantially smaller, and
is substantially smaller, and 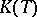 simplifies at the same time.
simplifies at the same time.
The space 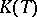 contains all functions of finite support, and the set of elements of the basis
contains all functions of finite support, and the set of elements of the basis 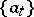 is the bijective inverse image of the set of functions
is the bijective inverse image of the set of functions 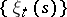 with only one non-zero value which is equal to one:
with only one non-zero value which is equal to one:
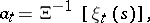 |
where 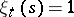 if
if 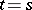 , and
, and 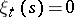 if
if 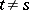 . In other words,
. In other words, 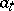 is the generator of a one-dimensional subspace
is the generator of a one-dimensional subspace 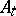 which is complementary in
which is complementary in 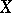 to the hyperplane defined by the equation
to the hyperplane defined by the equation 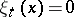 .
.
Thus, the role of the basis 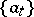 is to organize, out of the set of components
is to organize, out of the set of components 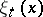 which constitute the image of
which constitute the image of  under the basis mapping, a summable (in some sense) set
under the basis mapping, a summable (in some sense) set 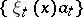 , i.e. a basis "decomposes" a space
, i.e. a basis "decomposes" a space 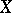 into a (generalized) direct sum of one-dimensional subspaces:
into a (generalized) direct sum of one-dimensional subspaces:
 |
A basis is defined in a similar manner in vector spaces with a uniform, limit (pseudo-topological), linear (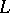 -), proximity, or other complementary structure.
-), proximity, or other complementary structure.
Generalizations of the concept of a basis may be and in fact have been given in various directions. Thus, the introduction of a topology and a measure on 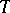 leads to the concept of the so-called continuous sum of elements from
leads to the concept of the so-called continuous sum of elements from 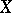 and to corresponding integral representations; the decomposition of the space
and to corresponding integral representations; the decomposition of the space 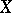 into (not necessarily one-dimensional) components is used in the spectral theory of linear operators; the consideration of arbitrary topological algebras over a field
into (not necessarily one-dimensional) components is used in the spectral theory of linear operators; the consideration of arbitrary topological algebras over a field 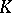 (e.g. algebras of measures on
(e.g. algebras of measures on 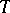 with values in
with values in 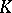 or even in
or even in 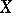 , algebras of projection operators, etc.) instead of
, algebras of projection operators, etc.) instead of 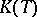 makes it possible to concretize many notions of abstract duality for topological vector spaces and, in particular, to employ the well-developed apparatus of the theory of characters.
makes it possible to concretize many notions of abstract duality for topological vector spaces and, in particular, to employ the well-developed apparatus of the theory of characters.
A countable basis, which is the most extensively studied and, from the practical point of view, the most important example of a basis, is a sequence 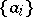 of elements of a space
of elements of a space 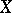 such that each element
such that each element  is in unique correspondence with its series expansion with respect to the basis
is in unique correspondence with its series expansion with respect to the basis 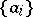
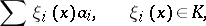 |
which (in the topology of 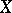 ) converges to
) converges to  . Here,
. Here, 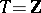 , and there exists a natural order in it. A countable basis is often simply called a "basis" . A weak countable basis is defined in an analogous manner if weak convergence of the expansion is understood. For instance, the functions
, and there exists a natural order in it. A countable basis is often simply called a "basis" . A weak countable basis is defined in an analogous manner if weak convergence of the expansion is understood. For instance, the functions 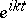 ,
, 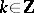 , form a basis in the spaces
, form a basis in the spaces 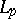 ,
, 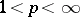 (periodic functions absolutely summable of degree
(periodic functions absolutely summable of degree 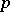 ); on the contrary, these functions do not form a basis in the spaces
); on the contrary, these functions do not form a basis in the spaces 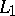 ,
, 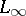 (measurable functions which almost everywhere coincide with bounded functions) or
(measurable functions which almost everywhere coincide with bounded functions) or 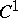 (continuous periodic functions). A necessary, but by far not sufficient, condition for the existence of a countable basis is the separability of
(continuous periodic functions). A necessary, but by far not sufficient, condition for the existence of a countable basis is the separability of 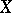 (e.g. a countable basis cannot exist in the space of measurable functions on an interval
(e.g. a countable basis cannot exist in the space of measurable functions on an interval 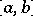 with values in
with values in 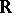 ). Moreover, the space
). Moreover, the space 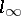 of bounded sequences, not being separable in the topology of
of bounded sequences, not being separable in the topology of 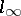 , has no countable basis, but the elements
, has no countable basis, but the elements 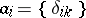 , where
, where 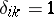 if
if 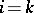 , and
, and 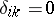 if
if 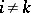 , form a basis in the weak topology
, form a basis in the weak topology 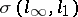 . The question of the existence of a countable basis in separable Banach spaces (the basis problem) has been negatively solved [6]. The analogous problem for nuclear spaces also has a negative solution [7].
. The question of the existence of a countable basis in separable Banach spaces (the basis problem) has been negatively solved [6]. The analogous problem for nuclear spaces also has a negative solution [7].
A countable basis is, however, not always "well-suited" for applications. For example, the components 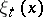 may be discontinuous, the expansion of
may be discontinuous, the expansion of  need not converge unconditionally, etc. In this connection one puts restrictions on the basis or introduces generalizations of it.
need not converge unconditionally, etc. In this connection one puts restrictions on the basis or introduces generalizations of it.
A basis of countable type is one of the generalizations of the concept of a countable basis in which, although 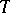 is not countable, nevertheless the decomposition of
is not countable, nevertheless the decomposition of 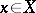 with respect to it has a natural definition: the corresponding space
with respect to it has a natural definition: the corresponding space 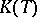 consists of functions with countable support. For instance, a complete orthonormal set
consists of functions with countable support. For instance, a complete orthonormal set 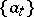 in a Hilbert space
in a Hilbert space 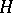 is a basis; if
is a basis; if 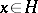 , then
, then 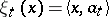 (where
(where 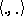 is the scalar product in
is the scalar product in 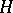 ) for all (except possibly a countable set of) indices
) for all (except possibly a countable set of) indices 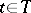 , and the series
, and the series 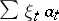 converges to
converges to  . The basis mapping is determined by the orthogonal projections onto the closed subspaces generated by the elements
. The basis mapping is determined by the orthogonal projections onto the closed subspaces generated by the elements 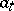 . A basis of the space
. A basis of the space 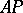 of all complex-valued almost-periodic functions on
of all complex-valued almost-periodic functions on 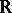 consists of the functions
consists of the functions 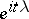 ; here,
; here, 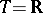 ,
, 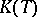 is the set of countably-valued functions, and the basis mapping is defined by the formula:
is the set of countably-valued functions, and the basis mapping is defined by the formula:
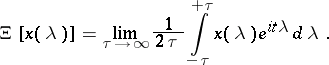 |
An unconditional basis is a countable basis in a space 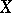 such that the decomposition of any element
such that the decomposition of any element  converges unconditionally (i.e. the sum of the series does not change if an arbitrary number of its terms is rearranged). For instance, in
converges unconditionally (i.e. the sum of the series does not change if an arbitrary number of its terms is rearranged). For instance, in 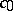 (sequences converging to zero) and
(sequences converging to zero) and 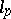 (sequences summable of degree
(sequences summable of degree 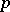 ,
, 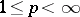 ) the elements
) the elements 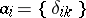 form an unconditional basis; in the space
form an unconditional basis; in the space 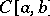 of continuous functions on the interval
of continuous functions on the interval 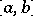 no basis can be unconditional. An orthonormal countable basis of a Hilbert space is an unconditional basis. A Banach space with an unconditional basis is weakly complete (accordingly, it has a separable dual space) if and only if it contains no subspace isomorphic to
no basis can be unconditional. An orthonormal countable basis of a Hilbert space is an unconditional basis. A Banach space with an unconditional basis is weakly complete (accordingly, it has a separable dual space) if and only if it contains no subspace isomorphic to 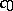 (or, correspondingly,
(or, correspondingly, 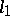 ).
).
Two bases 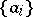 and
and 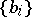 of the Banach spaces
of the Banach spaces 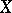 and
and 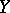 , respectively, are said to be equivalent if there exists a bijective linear mapping
, respectively, are said to be equivalent if there exists a bijective linear mapping  that can be extended to an isomorphism between
that can be extended to an isomorphism between 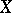 and
and 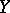 ; these bases are said to be quasi-equivalent if they become equivalent as a result of a certain rearrangement and normalization of the elements of one of them. In each of the spaces,
; these bases are said to be quasi-equivalent if they become equivalent as a result of a certain rearrangement and normalization of the elements of one of them. In each of the spaces, 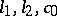 all normalized unconditional bases are equivalent. However, there exist normalized bases not equivalent to orthonormal ones.
all normalized unconditional bases are equivalent. However, there exist normalized bases not equivalent to orthonormal ones.
A summable basis — a generalization of the concept of an unconditional basis corresponding to a set 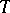 of arbitrary cardinality and becoming identical with it if
of arbitrary cardinality and becoming identical with it if 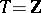 — is a set
— is a set 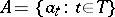 such that for an arbitrary element
such that for an arbitrary element  there exists a set of linear combinations (partial sums) of elements from
there exists a set of linear combinations (partial sums) of elements from 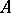 , which is called a generalized decomposition of
, which is called a generalized decomposition of  , which is summable to
, which is summable to  . This means that for any neighbourhood
. This means that for any neighbourhood 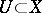 of zero it is possible to find a finite subset
of zero it is possible to find a finite subset 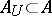 such that for any finite set
such that for any finite set 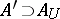 the relation
the relation
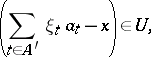 |
is true, i.e. when the partial sums form a Cauchy system (Cauchy filter). For instance, an arbitrary orthonormal basis of a Hilbert space is a summable basis. A weakly summable basis is defined in a similar way. A totally summable basis is a summable basis such that there exists a bounded set 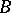 for which the set of semi-norms
for which the set of semi-norms 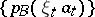 is summable. A totally summable basis is at most countable. In a dual nuclear space all weakly summable bases are totally summable.
is summable. A totally summable basis is at most countable. In a dual nuclear space all weakly summable bases are totally summable.
An absolute basis (absolutely summable basis) is a summable basis of a locally convex space over a normed field such that for any neighbourhood 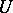 of zero and for each
of zero and for each 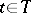 the family of semi-norms
the family of semi-norms 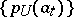 is summable. All unconditional countable bases are absolute, i.e. the series
is summable. All unconditional countable bases are absolute, i.e. the series 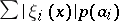 converges for all
converges for all 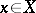 and all continuous semi-norms
and all continuous semi-norms 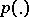 . Of all Banach spaces only the space
. Of all Banach spaces only the space 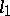 has an absolute countable basis. If a Fréchet space has an absolute basis, all its unconditional bases are absolute. In nuclear Fréchet spaces any countable basis (if it exists) is absolute [13].
has an absolute countable basis. If a Fréchet space has an absolute basis, all its unconditional bases are absolute. In nuclear Fréchet spaces any countable basis (if it exists) is absolute [13].
A Schauder basis is a basis 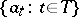 of a space
of a space 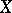 such that the basis mapping defined by it is continuous (and is therefore an isomorphism onto some space
such that the basis mapping defined by it is continuous (and is therefore an isomorphism onto some space 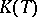 ), i.e. a basis in which the components
), i.e. a basis in which the components 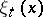 for any
for any 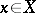 and, in particular, the coefficients of the decomposition of
and, in particular, the coefficients of the decomposition of  with respect to this basis, are continuous functionals on
with respect to this basis, are continuous functionals on 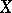 . This basis was first defined by J. Schauder [5] for the case
. This basis was first defined by J. Schauder [5] for the case 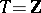 . The concept of a Schauder basis is the most important of all modifications of the concept of a basis.
. The concept of a Schauder basis is the most important of all modifications of the concept of a basis.
A Schauder basis is characterized by the fact that 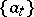 and
and 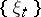 form a bi-orthogonal system. Thus, the sequences
form a bi-orthogonal system. Thus, the sequences 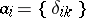 form countable Schauder bases in the spaces
form countable Schauder bases in the spaces 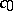 and
and 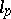 ,
, 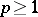 . A countable Schauder basis forms a Haar system in the space
. A countable Schauder basis forms a Haar system in the space 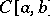 . In complete metric vector spaces (in particular, in Banach spaces) all countable bases are Schauder bases [10]. In Fréchet spaces the concept of a weak basis and a Schauder basis are identical [11]. In barrelled spaces in which there are no linear continuous functionals, there is also no Schauder basis [8]. However, if a weak Schauder basis exists in these spaces, it is an ordinary Schauder basis [9]. A barrelled locally convex space with a countable Schauder basis is reflexive if and only if this basis is at the same time a shrinking set, i.e. if the
. In complete metric vector spaces (in particular, in Banach spaces) all countable bases are Schauder bases [10]. In Fréchet spaces the concept of a weak basis and a Schauder basis are identical [11]. In barrelled spaces in which there are no linear continuous functionals, there is also no Schauder basis [8]. However, if a weak Schauder basis exists in these spaces, it is an ordinary Schauder basis [9]. A barrelled locally convex space with a countable Schauder basis is reflexive if and only if this basis is at the same time a shrinking set, i.e. if the 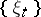 corresponding to it will be a basis in the dual space
corresponding to it will be a basis in the dual space 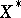 and will be boundedly complete, i.e. if the boundedness of the set of partial sums of a series
and will be boundedly complete, i.e. if the boundedness of the set of partial sums of a series 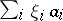 implies that this series is convergent [12]. If a Schauder basis is an unconditional basis in a Banach space, then it is a shrinking set (or a boundedly complete set) if and only if
implies that this series is convergent [12]. If a Schauder basis is an unconditional basis in a Banach space, then it is a shrinking set (or a boundedly complete set) if and only if 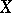 does not contain subspaces isomorphic to
does not contain subspaces isomorphic to 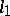 (or, respectively, to
(or, respectively, to 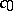 ).
).
A Schauder basis in a locally convex space is equicontinuous if for any neighbourhood 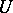 of zero it is possible to find a neighbourhood
of zero it is possible to find a neighbourhood 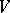 of zero such that
of zero such that
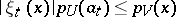 |
for all 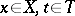 . All Schauder bases of a barrelled space are equicontinuous, and each complete locally convex space with a countable equicontinuous basis can be identified with some sequence space [15]. An equicontinuous basis of a nuclear space is absolute.
. All Schauder bases of a barrelled space are equicontinuous, and each complete locally convex space with a countable equicontinuous basis can be identified with some sequence space [15]. An equicontinuous basis of a nuclear space is absolute.
References
| [1] | P.M. Cohn, "Universal algebra" , Reidel (1981) |
| [2] | A.I. Mal'tsev, "Algebraic systems" , Springer (1973) (Translated from Russian) |
| [3] | N. Bourbaki, "Elements of mathematics. Algebra: Algebraic structures. Linear algebra" , 1 , Addison-Wesley (1974) pp. Chapt.1;2 (Translated from French) |
| [4] | G. Hamel, "Eine Basis aller Zahlen und die unstetigen Lösungen der Funktionalgleichung: 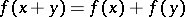 " Math. Ann. , 60 (1905) pp. 459–462 " Math. Ann. , 60 (1905) pp. 459–462 |
| [5] | J. Schauder, "Zur Theorie stetiger Abbildungen in Funktionalräumen" Math. Z. , 26 (1927) pp. 47–65; 417–431 |
| [6] | P. Enflo, "A counterexample to the approximation problem in Banach spaces" Acta Math. , 130 (1973) pp. 309–317 |
| [7] | N.M. Zobin, B.S. Mityagin, "Examples of nuclear linear metric spaces without a basis" Functional Anal. Appl. , 8 : 4 (1974) pp. 304–313 Funktsional. Analiz. i Prilozhen. , 8 : 4 (1974) pp. 35–47 |
| [8] | R.E. Edwards, "Functional analysis: theory and applications" , Holt, Rinehart & Winston (1965) |
| [9] | J. Dieudonné, "Sur les espaces de Köthe" J. d'Anal. Math. , 1 (1951) pp. 81–115 |
| [10] | M.G. Arsove, "The Paley-Wiener theorem in metric linear spaces" Pacific J. Math. , 10 (1960) pp. 365–379 |
| [11] | C. Bessaga, A. Pelczyński, "Spaces of continuous functions IV" Studia Math. , 19 (1960) pp. 53–62 |
| [12] | R.C. James, "Bases and reflexivity in Banach spaces" Ann. of Math. (2) , 52 : 3 (1950) pp. 518–527 |
| [13] | A. Dynin, B. Mityagin, "Criterion for nuclearity in terms of approximate dimension" Bull. Acad. Polon. Sci. Sér. Sci. Math., Astr. Phys. , 8 (1960) pp. 535–540 |
| [14] | M.M. Day, "Normed linear spaces" , Springer (1958) |
| [15] | A. Pietsch, "Nuclear locally convex spaces" , Springer (1972) (Translated from German) |
| [16] | I.M. Singer, "Bases in Banach spaces" , 1–2 , Springer (1970–1981) |
Basis. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Basis&oldid=13389