Base

of a topological space 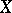, base of a topology, basis of a topology, open base

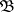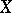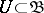A family of open subsets of such that each open subset is a union of subcollections . The concept of a base is a fundamental concept in topology: in many problems concerned with open sets of some space it is sufficient to restrict the considerations to its base. A space can have many bases, the largest one of which is the family of all open sets. The minimum of the cardinalities of all bases is called the weight of the topological space . In a space of weight there exists an everywhere-dense set of cardinality 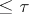. Spaces with a countable base are also referred to as spaces satisfying the second axiom of countability. The dual concept of a closed base, formed by the complements of the elements of a base, is not used to any significant extent.

A local base of a space 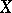at a point (a base of the point ) is a family of open sets of 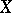with the following property: For any neighbourhood of it is possible to find an element 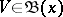such that 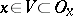. Spaces with a countable local base at every point are also referred to as spaces satisfying the first axiom of countability. A family 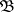of open sets in 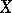is a base if and only if it is a local base of each one of its points .

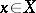Let 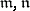be cardinal numbers. A base 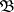of the space 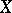is called an 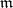-point base if each point 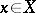belongs to at most 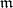elements of the family 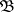; in particular, if 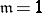, the base is called disjoint; if 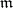is finite, it is called bounded point finite; and if 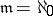, it is called point countable.

A base 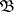of the space 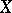is called 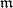-local if each point 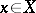has a neighbourhood 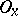intersecting with at most 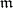elements of the family 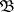; in particular, if 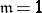, the base is referred to as discrete; if 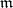is finite, it is called bounded locally finite; and if 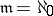, it is called locally countable. A base 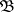is called an 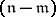-point base (or an 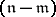-local base) if it is a union of a set of cardinality of 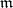-point (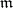-local) bases; examples are, for 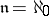, 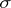-disjoint, 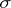-point finite, 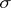-discrete and 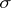-locally finite bases.

These concepts are used mainly in the criteria of metrizable spaces. Thus, a regular space with a countable base, or satisfying the first axiom of countability and with a point countable base, is metrizable; a regular space with a 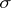-discrete or 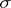-locally finite base is metrizable (the converse proposition is true in the former case only).

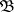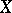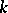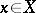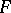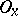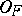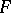A base of the space is called uniform (-uniform) if for each point (each compact subset ) and for each one of the neighbourhoods () only a finite number of elements of the base contain (intersect with ) and at the same time intersect with the complement 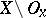(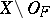). A space 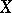is metrizable if and only if it is paracompact with a uniform base (a Kolmogorov or 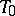-space with a 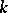-uniform base).

A base 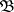of the space 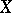is called regular if for each point 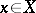and an arbitrary neighbourhood 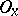of it there exists a neighbourhood 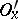such that the set of all the elements of the base which intersect both with 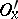and 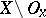is finite. An accessible or 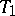-space is metrizable if and only if it has a regular base.

A generalization of the concept of a base is the so-called 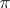-base (lattice base), which is a family 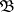of open sets in the space 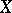such that each non-empty open set in 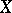contains a non-empty set from , i.e. 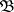is dense in 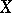according to Hausdorff. All bases are 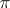-bases, but the converse is not true; thus, the set 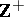in the Stone–Čech compactification of the set of natural numbers in 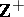forms only a 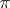-base.

References

[1]	P.S. Aleksandrov, "Einführung in die Mengenlehre und die Theorie der reellen Funktionen" , Deutsch. Verlag Wissenschaft. (1956) (Translated from Russian)
[2]	P.S. [P.S. Uryson] Urysohn, , Works on topology and other fields of mathematics , 1–2 , Leningrad (1951) (In Russian)
[3]	P.S. Aleksandrov, B.A. Pasynkov, "An introduction to the theory of topological spaces and general dimension theory" , Moscow (1973) (In Russian)
[4]	A.V. Arkhangel'skii, V.I. Ponomarev, "Fundamentals of general topology: problems and exercises" , Reidel (1984) (Translated from Russian)
[5]	N. Bourbaki, "Elements of mathematics. General topology" , Addison-Wesley (1966) (Translated from French)

Comments

Closed bases are useful in compactification theory, cf. Compactification.

Besides the notions of a bounded point-finite base and a bounded local-finite base one also uses that of a point-finite base and a local-finite base. A base (or any family of subsets 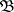) is called point finite if every point belongs to finitely many members of 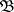, i.e. if 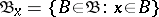is finite for every . Note that the families 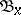can have arbitrary large finite cardinalities, in contrast to the definition of bounded point finiteness, when the cardinalities of 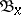are bounded by a fixed finite 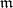. Similar remarks apply to local finiteness.