Banach space
B-space
A complete normed vector space. The function spaces introduced by D. Hilbert, M. Fréchet and F. Riesz between 1904 and 1918 served as the starting point for the theory of Banach spaces. It is in these spaces that the fundamental concepts of strong and weak convergence, compactness, linear functional, linear operator, etc., were originally studied. Banach spaces were named after S. Banach who in 1922 began a systematic study of these spaces, based on axioms introduced by himself, and who obtained highly advanced results.
The theory of Banach spaces developed in parallel with the general theory of linear topological spaces (cf. Linear topological space). These theories mutually enriched one another with new ideas and facts. Thus, the idea of semi-norms, taken from the theory of normed spaces, became an indispensable tool in constructing the theory of locally convex linear topological spaces. The ideas of weak convergence of elements and linear functionals in Banach spaces ultimately evolved to the concept of weak topology. The theory of Banach spaces is a thoroughly studied branch of functional analysis, with numerous applications in various branches of mathematics — directly or by way of the theory of operators.
The problems involved in Banach spaces are of different types: the geometry of the unit ball, the geometry of subspaces, the linear topological classification, series and sequences in Banach spaces, best approximations in Banach spaces, functions with values in a Banach space, etc. Regarding the theory of operators in Banach spaces it should be pointed out that many theorems are directly related to the geometry and the topology of Banach spaces.
Examples. The Banach spaces encountered in analysis are mostly sets of functions or sequences of numbers which are subject to certain conditions.
1) 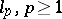 , is the space of numerical sequences
, is the space of numerical sequences  for which
for which
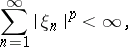 |
with the norm
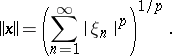 |
2) 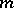 is the space of bounded numerical sequences with the norm
is the space of bounded numerical sequences with the norm
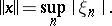 |
3)  is the space of convergent numerical sequences with the norm
is the space of convergent numerical sequences with the norm
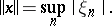 |
4) 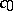 is the space of numerical sequences which converge to zero with the norm
is the space of numerical sequences which converge to zero with the norm
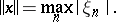 |
5) 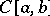 is the space of continuous functions
is the space of continuous functions 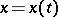 on
on 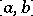 with the norm
with the norm
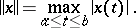 |
6) 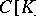 is the space of continuous functions on a compactum
is the space of continuous functions on a compactum 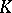 with the norm
with the norm
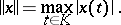 |
7) 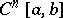 is the space of functions with continuous derivatives up to and including the order
is the space of functions with continuous derivatives up to and including the order  , with the norm
, with the norm
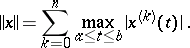 |
8) 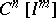 is the space of all functions defined in an
is the space of all functions defined in an 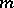 -dimensional cube that are continuously differentiable up to and including the order
-dimensional cube that are continuously differentiable up to and including the order  , with the norm of uniform boundedness in all derivatives of order at most
, with the norm of uniform boundedness in all derivatives of order at most  .
.
9) 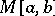 is the space of bounded measurable functions with the norm
is the space of bounded measurable functions with the norm
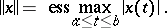 |
10) 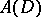 is the space of functions which are analytic in the open unit disc
is the space of functions which are analytic in the open unit disc 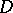 and are continuous in the closed disc
and are continuous in the closed disc 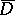 , with the norm
, with the norm
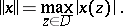 |
11) 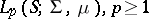 , is the space of functions
, is the space of functions 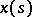 defined on a set
defined on a set 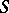 provided with a countably-additive measure
provided with a countably-additive measure 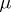 , with the norm
, with the norm
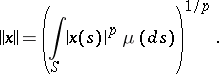 |
12) 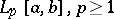 , is a special case of the space
, is a special case of the space 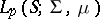 . It is the space of Lebesgue-measurable functions, summable of degree
. It is the space of Lebesgue-measurable functions, summable of degree 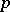 , with the norm
, with the norm
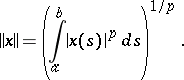 |
13) 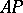 is the Bohr space of almost-periodic functions, with the norm
is the Bohr space of almost-periodic functions, with the norm
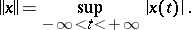 |
The spaces 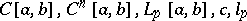 are separable; the spaces
are separable; the spaces 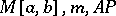 are non-separable;
are non-separable; 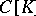 is separable if and only if
is separable if and only if 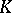 is a compact metric space.
is a compact metric space.
A (closed linear) subspace 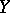 of a Banach space, considered apart from the enveloping space
of a Banach space, considered apart from the enveloping space 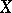 , is a Banach space. The quotient space
, is a Banach space. The quotient space 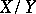 of a normed space by a subspace
of a normed space by a subspace 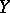 is a normed space if the norm is defined as follows. Let
is a normed space if the norm is defined as follows. Let 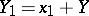 be a coset. Then
be a coset. Then
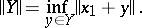 |
If 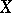 is a Banach space, then
is a Banach space, then 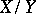 is a Banach space as well. The set of all continuous linear functionals defined on the normed space
is a Banach space as well. The set of all continuous linear functionals defined on the normed space 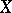 , with the norm
, with the norm
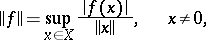 |
is said to be the dual space of 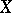 , and is denoted by
, and is denoted by 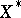 . It is a Banach space.
. It is a Banach space.
Banach spaces satisfy the Hahn–Banach theorem on the extension of linear functionals: If a linear functional is defined on a subspace 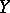 of a normed space
of a normed space 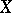 , it can be extended, while preserving its linearity and continuity, onto the whole space
, it can be extended, while preserving its linearity and continuity, onto the whole space 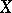 . Moreover, the extension can be made to have the same norm:
. Moreover, the extension can be made to have the same norm:
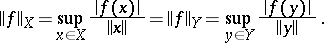 |
Even a more general theorem is valid: Let a real-valued function 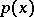 defined on a linear space satisfy the conditions:
defined on a linear space satisfy the conditions:
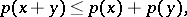 |
 |
and let 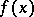 be a real-valued linear functional defined on a subspace
be a real-valued linear functional defined on a subspace 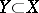 and such that
and such that
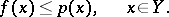 |
Then there exists a linear functional 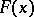 defined on the whole of
defined on the whole of 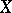 such that
such that
 |
A consequence of the Hahn–Banach theorem is the "inverse" formula which relates the norms of 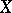 and
and 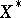 :
:
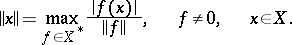 |
The maximum in this formula is attained for some 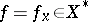 . Another important consequence is the existence of a separating set of continuous linear functionals, meaning that for any
. Another important consequence is the existence of a separating set of continuous linear functionals, meaning that for any 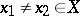 there exists a linear functional
there exists a linear functional 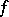 on
on 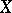 such that
such that 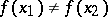 (cf. Complete set of functionals).
(cf. Complete set of functionals).
The general form of a linear functional is known for many specific Banach spaces. Thus, on 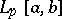 ,
, 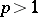 , all linear functionals are given by a formula
, all linear functionals are given by a formula
 |
where 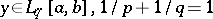 , and any function
, and any function 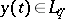 defines a linear functional
defines a linear functional 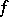 by this formula, moreover
by this formula, moreover
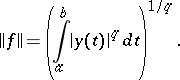 |
Thus, the dual space of 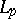 is
is 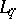 :
: 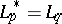 . Linear functionals on
. Linear functionals on 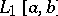 are defined by the same formula, but in this case
are defined by the same formula, but in this case 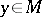 , so that
, so that  .
.
The space 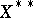 , dual to
, dual to 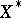 , is said to be the second dual. Third, fourth, etc., dual spaces are defined in a similar manner. Each element in
, is said to be the second dual. Third, fourth, etc., dual spaces are defined in a similar manner. Each element in 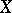 may be identified with some linear functional defined on
may be identified with some linear functional defined on 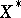 :
:
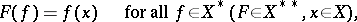 |
where  . One may then regard
. One may then regard 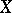 as a subspace of the space
as a subspace of the space 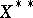 and
and 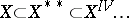 ,
, 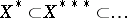 . If, as a result of these inclusions, the Banach space coincides with its second dual, it is called reflexive. In such a case all inclusions are equalities. If
. If, as a result of these inclusions, the Banach space coincides with its second dual, it is called reflexive. In such a case all inclusions are equalities. If 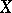 is not reflexive, all inclusions are strict. If the quotient space
is not reflexive, all inclusions are strict. If the quotient space 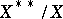 has finite dimension
has finite dimension  ,
, 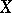 is said to be quasi-reflexive of order
is said to be quasi-reflexive of order  . Quasi-reflexive spaces exist for all
. Quasi-reflexive spaces exist for all  .
.
Reflexivity criteria for Banach spaces.
1) 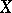 is reflexive if and only if for each
is reflexive if and only if for each 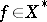 it is possible to find an
it is possible to find an 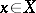 on which the "sup" in the formula
on which the "sup" in the formula
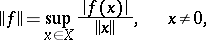 |
is attained.
2) In reflexive Banach spaces and only in such spaces each bounded set is relatively compact with respect to weak convergence: Any one of its infinite parts contains a weakly convergent sequence (the Eberlein–Shmul'yan theorem). The spaces 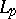 and
and 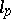 ,
, 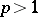 , are reflexive. The spaces
, are reflexive. The spaces 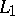 ,
, 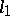 ,
, 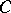 ,
,  ,
,  ,
, 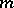 ,
, 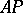 are non-reflexive.
are non-reflexive.
A Banach space is said to be weakly complete if each weak Cauchy sequence in it weakly converges to an element of the space. Every reflexive space is weakly complete. Moreover, the Banach spaces 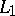 and
and 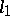 are weakly complete. The Banach spaces not containing a subspace isomorphic to
are weakly complete. The Banach spaces not containing a subspace isomorphic to 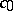 form an even wider class. These spaces resemble weakly-complete spaces in several respects.
form an even wider class. These spaces resemble weakly-complete spaces in several respects.
A Banach space is said to be strictly convex if its unit sphere 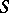 contains no segments. Convexity moduli are introduced for a quantitative estimation of the convexity of the unit sphere; these are the local convexity modulus
contains no segments. Convexity moduli are introduced for a quantitative estimation of the convexity of the unit sphere; these are the local convexity modulus
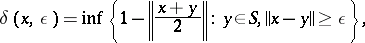 |
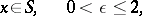 |
and the uniform convexity modulus
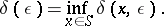 |
If 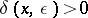 for all
for all 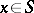 and all
and all 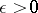 , the Banach space is said to be locally uniformly convex. If
, the Banach space is said to be locally uniformly convex. If 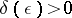 , the space is said to be uniformly convex. All uniformly convex Banach spaces are locally uniformly convex; all locally uniformly convex Banach spaces are strictly convex. In finite-dimensional Banach spaces the converses are also true. If a Banach space is uniformly convex, it is reflexive.
, the space is said to be uniformly convex. All uniformly convex Banach spaces are locally uniformly convex; all locally uniformly convex Banach spaces are strictly convex. In finite-dimensional Banach spaces the converses are also true. If a Banach space is uniformly convex, it is reflexive.
A Banach space is said to be smooth if for any linearly independent elements  and
and 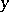 the function
the function 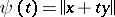 is differentiable for all values of
is differentiable for all values of 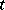 . A Banach space is said to be uniformly smooth if its modulus of smoothness
. A Banach space is said to be uniformly smooth if its modulus of smoothness
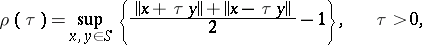 |
satisfies the condition
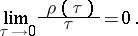 |
In uniformly smooth spaces, and only in such spaces, the norm is uniformly Fréchet differentiable. A uniformly smooth Banach space is smooth. The converse is true if the Banach space is finite-dimensional. A Banach space 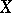 is uniformly convex (uniformly smooth) if and only if
is uniformly convex (uniformly smooth) if and only if 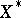 is uniformly smooth (uniformly convex). The following relationship relates the convexity modulus of a Banach space
is uniformly smooth (uniformly convex). The following relationship relates the convexity modulus of a Banach space 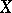 and the smoothness modulus of
and the smoothness modulus of 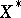 :
:
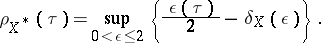 |
If a Banach space is uniformly convex (uniformly smooth), so are all its subspaces and quotient spaces. The Banach spaces  and
and  ,
, 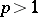 , are uniformly convex and uniformly smooth, and
, are uniformly convex and uniformly smooth, and
 |
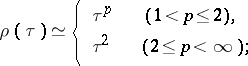 |
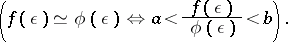 |
The Banach spaces 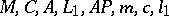 are not strictly convex and are not smooth.
are not strictly convex and are not smooth.
The following important theorems for linear operators are valid in Banach spaces:
The Banach–Steinhaus theorem. If a family of linear operators 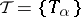 is bounded at each point,
is bounded at each point,
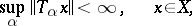 |
then it is norm-bounded:
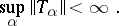 |
The Banach open-mapping theorem. If a linear continuous operator maps a Banach space  onto a Banach space
onto a Banach space  in a one-to-one correspondence, the inverse operator
in a one-to-one correspondence, the inverse operator 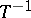 is also continuous.
is also continuous.
The closed-graph theorem. If a closed linear operator maps a Banach space 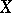 into a Banach space
into a Banach space 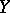 , then it is continuous.
, then it is continuous.
Isometries between Banach spaces occur rarely. The classical example is given by the Banach spaces 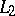 and
and 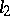 . The Banach spaces
. The Banach spaces 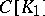 and
and 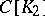 are isometric if and only if
are isometric if and only if 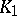 and
and 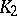 are homeomorphic (the Banach–Stone theorem). A measure of proximity of isomorphic Banach spaces is the number
are homeomorphic (the Banach–Stone theorem). A measure of proximity of isomorphic Banach spaces is the number
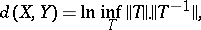 |
where 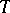 runs through all possible operators which realize a (linear topological) isomorphism between
runs through all possible operators which realize a (linear topological) isomorphism between 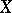 and
and 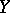 . If
. If 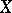 is isometric to
is isometric to 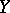 , then
, then 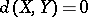 . However, non-isometric spaces for which
. However, non-isometric spaces for which 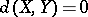 also exist; they are said to be almost-isometric. The properties of Banach spaces preserved under an isomorphism are said to be linear topological. They include separability, reflexivity and weak completeness. The isomorphic classification of Banach spaces contains, in particular, the following theorems:
also exist; they are said to be almost-isometric. The properties of Banach spaces preserved under an isomorphism are said to be linear topological. They include separability, reflexivity and weak completeness. The isomorphic classification of Banach spaces contains, in particular, the following theorems:
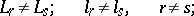 |
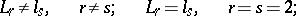 |
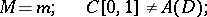 |
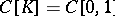 if
if 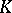 is a metric compactum with the cardinality of the continuum;
is a metric compactum with the cardinality of the continuum;
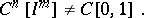 |
Each separable Banach space is isomorphic to a locally uniformly convex Banach space. It is not known (1985) if there are Banach spaces which are isomorphic to none of their hyperplanes. There exist Banach spaces which are not isomorphic to strictly convex spaces. Irrespective of the linear nature of normed spaces, it is possible to consider their topological classification. Two spaces are homeomorphic if a one-to-one continuous correspondence, such that its inverse is also continuous, can be established between their elements. An incomplete normed space is not homeomorphic to any Banach space. All infinite-dimensional separable Banach spaces are homeomorphic.
In the class of separable Banach spaces, 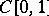 and
and 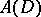 are universal (cf. Universal space). The class of reflexive separable Banach spaces contains even no isomorphic universal spaces. The Banach space
are universal (cf. Universal space). The class of reflexive separable Banach spaces contains even no isomorphic universal spaces. The Banach space 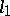 is universal in a somewhat different sense: All separable Banach spaces are isometric to one of its quotient spaces.
is universal in a somewhat different sense: All separable Banach spaces are isometric to one of its quotient spaces.
Each of the Banach spaces mentioned above, except 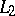 and
and 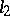 , contains subspaces without a complement. In particular, in
, contains subspaces without a complement. In particular, in 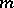 and
and 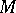 every infinite-dimensional separable subspace is non-complementable, while in
every infinite-dimensional separable subspace is non-complementable, while in 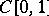 all infinite-dimensional reflexive subspaces are non-complementable. If all subspaces in a Banach space are complementable, the space is isomorphic to a Hilbert space. It is not known (1985) whether or not all Banach spaces are direct sums of some two infinite-dimensional subspaces. A subspace
all infinite-dimensional reflexive subspaces are non-complementable. If all subspaces in a Banach space are complementable, the space is isomorphic to a Hilbert space. It is not known (1985) whether or not all Banach spaces are direct sums of some two infinite-dimensional subspaces. A subspace 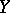 is complementable if and only if there exists a projection which maps
is complementable if and only if there exists a projection which maps 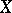 onto
onto 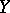 . The lower bound of the norms of the projections on
. The lower bound of the norms of the projections on 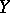 is called the relative projection constant
is called the relative projection constant 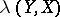 of the subspace
of the subspace 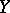 in
in 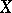 . Each
. Each  -dimensional subspace of a Banach space is complementable and
-dimensional subspace of a Banach space is complementable and 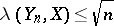 . The absolute projection constant
. The absolute projection constant 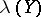 of a Banach space
of a Banach space 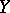 is
is
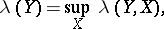 |
where 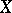 runs through all Banach spaces which contain
runs through all Banach spaces which contain 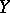 as a subspace. For any infinite-dimensional separable Banach space
as a subspace. For any infinite-dimensional separable Banach space 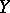 one has
one has 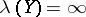 . Banach spaces for which
. Banach spaces for which 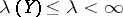 form the class
form the class 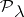 (
(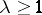 ). The class
). The class 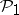 coincides with the class of spaces
coincides with the class of spaces 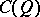 where
where 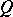 are extremally-disconnected compacta (cf. Extremally-disconnected space).
are extremally-disconnected compacta (cf. Extremally-disconnected space).
Fundamental theorems on finite-dimensional Banach spaces. 1) A finite-dimensional space (a Minkowski space) is complete, i.e. is a Banach space. 2) All linear operators in a finite-dimensional Banach space are continuous. 3) A finite-dimensional Banach space is reflexive (the dimension of 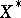 is equal to the dimension of
is equal to the dimension of 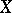 ). 4) A Banach space is finite-dimensional if and only if its unit ball is compact. 5) All
). 4) A Banach space is finite-dimensional if and only if its unit ball is compact. 5) All  -dimensional Banach spaces are pairwise isomorphic; their set becomes compact if one introduces the distance
-dimensional Banach spaces are pairwise isomorphic; their set becomes compact if one introduces the distance
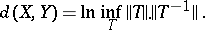 |
A series
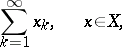 | (*) |
is said to be convergent if there exists a limit 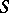 of the sequence of partial sums:
of the sequence of partial sums:
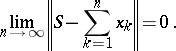 |
If
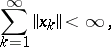 |
the series (*) is convergent, and is said in such a case to be absolutely convergent. A series is said to be unconditionally convergent if it converges when its terms are arbitrarily rearranged. The sum of an absolutely convergent series is independent of the arrangement of its terms. In the case of series in a finite-dimensional space (and, in particular, for series of numbers) unconditional and absolute convergence are equivalent. In infinite-dimensional Banach spaces unconditional convergence follows from absolute convergence but the converse is not true in any infinite-dimensional Banach space. This is a consequence of the Dvoretskii–Rogers theorem: For all numbers 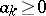 , subject to the condition
, subject to the condition 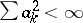 , there exists in each infinite-dimensional Banach space an unconditionally convergent series
, there exists in each infinite-dimensional Banach space an unconditionally convergent series 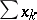 such that
such that  ,
, 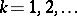 . In the space
. In the space 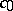 (and hence also in any Banach space containing a subspace isomorphic to
(and hence also in any Banach space containing a subspace isomorphic to 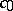 ), for any sequence
), for any sequence 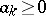 that converges to zero, there exists an unconditionally convergent series
that converges to zero, there exists an unconditionally convergent series 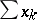 ,
,  . In
. In 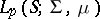 the unconditional convergence of the series
the unconditional convergence of the series 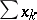 implies that
implies that
 |
where
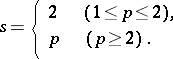 |
In a uniformly convex Banach space with convexity modulus 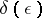 the unconditional convergence of the series
the unconditional convergence of the series 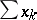 implies that
implies that
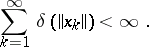 |
A series 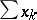 is said to be weakly unconditionally Cauchy if the series of numbers
is said to be weakly unconditionally Cauchy if the series of numbers 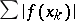 converges for each
converges for each 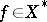 . Each weakly unconditionally Cauchy series in
. Each weakly unconditionally Cauchy series in 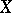 converges if and only if
converges if and only if 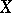 contains no subspace isomorphic to
contains no subspace isomorphic to 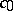 .
.
A sequence of elements 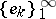 of a Banach space is said to be minimal if each one of its terms lies outside the closure of
of a Banach space is said to be minimal if each one of its terms lies outside the closure of 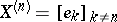 , the linear hull of the remaining elements. A sequence is said to be uniformly minimal if
, the linear hull of the remaining elements. A sequence is said to be uniformly minimal if
 |
If 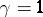 , the series is said to be an Auerbach system. In each
, the series is said to be an Auerbach system. In each  -dimensional Banach space there exists a complete Auerbach system
-dimensional Banach space there exists a complete Auerbach system 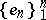 . It is not known (1985) whether or not a complete Auerbach system exists in each separable Banach space. For each minimal system there exists an adjoint system of linear functionals
. It is not known (1985) whether or not a complete Auerbach system exists in each separable Banach space. For each minimal system there exists an adjoint system of linear functionals 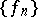 , which is connected with
, which is connected with  by the biorthogonality relations:
by the biorthogonality relations: 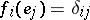 . In such a case the system
. In such a case the system 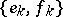 is said to be biorthogonal. A set of linear functionals is said to be total if it annihilates only the zero element of the space. In each separable Banach space there exists a complete, minimal system with a total adjoint. Each element
is said to be biorthogonal. A set of linear functionals is said to be total if it annihilates only the zero element of the space. In each separable Banach space there exists a complete, minimal system with a total adjoint. Each element 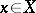 can formally be developed in a series by the biorthogonal system:
can formally be developed in a series by the biorthogonal system:
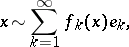 |
but in the general case this series is divergent.
A system of elements 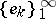 is said to be a basis in
is said to be a basis in 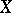 if each element
if each element 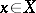 can be uniquely represented as a convergent series
can be uniquely represented as a convergent series
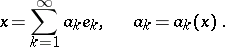 |
Each basis in a Banach space is a complete uniform minimal system with a total adjoint. The converse is not true, as can be seen from the example of the system 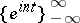 in
in 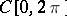 and
and 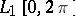 .
.
A basis is said to be unconditional if all its rearrangements are also bases; otherwise it is said to be conditional. The system 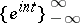 in
in 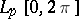 ,
, 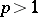 ,
, 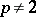 , is a conditional basis. The Haar system is an unconditional basis in
, is a conditional basis. The Haar system is an unconditional basis in 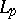 ,
, 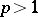 . There is no unconditional basis in the spaces
. There is no unconditional basis in the spaces 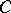 and
and 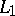 . It is not known (1985) whether or not each Banach space contains an infinite-dimensional subspace with an unconditional basis. Any non-reflexive Banach space with an unconditional basis contains a subspace isomorphic to
. It is not known (1985) whether or not each Banach space contains an infinite-dimensional subspace with an unconditional basis. Any non-reflexive Banach space with an unconditional basis contains a subspace isomorphic to 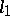 or
or  .
.
Two normalized bases 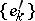 and
and 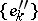 in two Banach spaces
in two Banach spaces 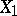 and
and 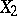 are said to be equivalent if the correspondence
are said to be equivalent if the correspondence 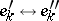 ,
, 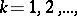 may be extended to an isomorphism between
may be extended to an isomorphism between 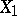 and
and 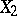 . In each of the spaces
. In each of the spaces 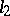 ,
, 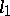 ,
,  all normalized unconditional bases are equivalent to the natural basis. Bases constructed in Banach spaces which have important applications are not always suitable for solving problems, e.g. in the theory of operators. T-bases, or summation bases, have been introduced in this context. Let
all normalized unconditional bases are equivalent to the natural basis. Bases constructed in Banach spaces which have important applications are not always suitable for solving problems, e.g. in the theory of operators. T-bases, or summation bases, have been introduced in this context. Let 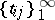 be the matrix of a regular summation method (cf. Regular summation methods). The system of elements
be the matrix of a regular summation method (cf. Regular summation methods). The system of elements 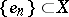 is said to be a
is said to be a 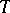 -basis corresponding to the given summation method if each
-basis corresponding to the given summation method if each 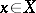 can be uniquely represented by a series
can be uniquely represented by a series
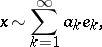 |
which is summable to  by this method. The trigonometric system
by this method. The trigonometric system 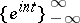 in
in  is a summation basis for the methods of Cesàro and Abel. Each
is a summation basis for the methods of Cesàro and Abel. Each 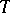 -basis is a complete minimal (not necessarily uniformly minimal) system with a total adjoint. The converse is not true. Until recently (the 1970's) one of the principal problems of the theory of Banach spaces was the basis problem dealt with by Banach himself: Does a basis exist in each separable Banach space? The question of existence of a basis in specifically defined Banach spaces remained open as well. The first example of a separable Banach space without a basis was constructed in 1972; bases in the spaces
-basis is a complete minimal (not necessarily uniformly minimal) system with a total adjoint. The converse is not true. Until recently (the 1970's) one of the principal problems of the theory of Banach spaces was the basis problem dealt with by Banach himself: Does a basis exist in each separable Banach space? The question of existence of a basis in specifically defined Banach spaces remained open as well. The first example of a separable Banach space without a basis was constructed in 1972; bases in the spaces 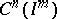 and
and 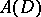 have been constructed.
have been constructed.
References
| [1] | S. Banach, "Sur les opérations dans les ensembles abstraits et leur application aux équations intégrales" Fund. Math. , 3 (1922) pp. 133–181 |
| [2] | S.S. Banach, "A course of functional analysis" , Kiev (1948) (In Ukrainian) |
| [3] | N. Dunford, J.T. Schwartz, "Linear operators. General theory" , 1 , Interscience (1958) |
| [4] | M.M. Day, "Normed linear spaces" , Springer (1958) |
| [5] | N. Bourbaki, "Elements of mathematics. Topological vector spaces" , Addison-Wesley (1977) (Translated from French) |
| [6] | I.M. Singer, "Bases in Banach spaces" , 1–2 , Springer (1970–1981) |
| [7] | J. Lindenstrauss, L. Tzafriri, "Classical Banach spaces" , 1–2 , Springer (1977–1979) |
| [8] | J.J. Diestel, "Geometry of Banach spaces. Selected topics" , Springer (1975) |
| [9] | B. Beauzamy, "Introduction to Banach spaces and their geometry" , North-Holland (1985) |
Comments
The second dual of a space is also called the bidual.
References
| [a1] | Z. Semanedi, "Banach spaces of continuous functions" , Polish Sci. Publ. (1971) |
Banach space. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Banach_space&oldid=11548