Banach limit
Banach limits originated in [a1], Chapt. II, Sect. 3. Denoting the positive integers by  , the set
, the set  is the real vector space of all bounded sequences of real numbers. For any element
is the real vector space of all bounded sequences of real numbers. For any element  , one defines
, one defines  by
by  for all
for all 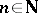 . S. Banach showed that there exists an element in the dual
. S. Banach showed that there exists an element in the dual  , called
, called  , such that
, such that
1)  for all
for all  ;
;
2) 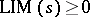 for all non-negative sequences
for all non-negative sequences 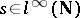 ;
;
3) 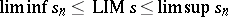 for all
for all 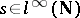 ;
;
4) 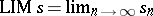 for all convergent sequences
for all convergent sequences 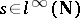 . Banach proved the existence of this generalized limit by using the Hahn–Banach theorem. Today (1996), Banach limits are studied via the notion of amenability.
. Banach proved the existence of this generalized limit by using the Hahn–Banach theorem. Today (1996), Banach limits are studied via the notion of amenability.
For a semi-group 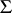 one defines
one defines 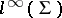 to be the real vector space of all real bounded functions on
to be the real vector space of all real bounded functions on 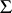 . For an element
. For an element  one denotes the left (respectively, right) shift by
one denotes the left (respectively, right) shift by  (respectively,
(respectively, 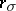 ). Thus,
). Thus, 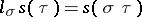 for all
for all  and
and 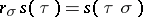 for all
for all 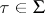 . An element
. An element 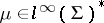 is called a left- (respectively right-) invariant mean if
is called a left- (respectively right-) invariant mean if
1) 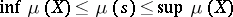 ;
;
2) 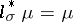 (respectively,
(respectively,  ), where, e.g.,
), where, e.g., 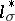 is the adjoint of
is the adjoint of 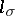 .
. 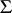 itself is called left (respectively, right) amenable if there exists a left- (respectively, right-) invariant mean in
itself is called left (respectively, right) amenable if there exists a left- (respectively, right-) invariant mean in 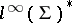 . The existence of Banach limits above is a special case of an invariant mean, where
. The existence of Banach limits above is a special case of an invariant mean, where  equals the semi-group of natural numbers. Banach also proved that the real numbers are amenable (left and right). M.M. Day has proved that every Abelian semi-group is left and right amenable. On the other hand,
equals the semi-group of natural numbers. Banach also proved that the real numbers are amenable (left and right). M.M. Day has proved that every Abelian semi-group is left and right amenable. On the other hand,  , the free group on two generators, is not amenable.
, the free group on two generators, is not amenable.
Another approach to amenability is the measure-theoretic point of view. In fact, the prehistory of amenability starts with the following question by H. Lebesgue in the classic "Leçons sur L'Intégration et la Recherche des Fonctions Primitives" ([a5], pp. 114–115): Can countable additivity of the Lebesgue measure be replaced by finite additivity? Banach answered the question in the negative, constructing a finitely additive measure on all subsets of the real numbers, invariant under translation, again using the Hahn–Banach theorem. More generally, if a group 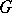 is acting on a set
is acting on a set 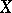 , a finitely additive probability measure on the collection of all subsets of
, a finitely additive probability measure on the collection of all subsets of 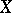 , invariant under
, invariant under 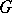 , is sometimes also called an invariant mean. If
, is sometimes also called an invariant mean. If 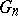 is the isometry group of
is the isometry group of 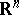 , one can ask for a finitely additive measure invariant under
, one can ask for a finitely additive measure invariant under 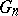 . Such a measure does exist for
. Such a measure does exist for 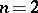 , but not for
, but not for 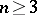 . For
. For 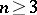 this leads to so-called paradoxical decompositions or the Banach–Tarski paradox (see Tarski problem; for a survey, see [a8]). For all
this leads to so-called paradoxical decompositions or the Banach–Tarski paradox (see Tarski problem; for a survey, see [a8]). For all 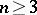 , the group
, the group 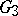 contains the non-amenable
contains the non-amenable 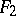 as a subgroup. It has been proved that the Banach–Tarski paradox is effectively (i.e., in ZF set theory) implied by the Hahn–Banach theorem (see [a7]).
as a subgroup. It has been proved that the Banach–Tarski paradox is effectively (i.e., in ZF set theory) implied by the Hahn–Banach theorem (see [a7]).
For a survey of results of the role of amenability, see [a6] and for a survey of the Hahn–Banach theorem, see [a2]. For the early history of Banach limits and invariant means, including many important results, see [a3] and [a4].
References
| [a1] | S. Banach, "Théorie des opérations linéaires" , PWN (1932) |
| [a2] | G. Buskes, "The Hahn–Banach theorem surveyed" Dissertationes Mathematicae , CCCXXVII (1993) |
| [a3] | M.M. Day, "Normed linear spaces" , Ergebnisse der Mathematik und ihrer Grenzgebiete , 21 , Springer (1973) |
| [a4] | Greenleaf, F.P, "Invariant means on topological groups and their applications" , v. Nostrand (1969) |
| [a5] | H. Lebesgue, "Oeuvres Scientifiques" , L'Enseign. Math. , II , Inst. Math. Univ. Genæve (1972) |
| [a6] | A.L.T. Paterson, "Amenibility" , Mathematical Surveys and Monographs , 29 , Amer. Math. Soc. (1988) |
| [a7] | J. Pawlikowski, "The Hahn–Banach theorem implies the Banach–Tarski paradox" Fundam. Math. , 138 (1991) pp. 20–22 |
| [a8] | S. Wagon, "The Banach–Tarski paradox" , Cambridge Univ. Press (1986) |
Banach limit. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Banach_limit&oldid=39373