Banach indicatrix
multiplicity function, of a continuous function $y=f(x)$, $a\leq x\leq b$
An integer-valued function $N(y,f)$, $-\infty < y < \infty$, equal to the number of roots of the equation $f(x)=y$. If, for a given value of $y$, this equation has an infinite number of roots, then $$ N(y,f) = +\infty, $$
and if it has no roots, then
$$ N(y,f) = 0. $$
The function $N(y,f)$ was defined by S. Banach [1] (see also [2]). He proved that the indicatrix $N(y,f)$ of any continuous function $f(x)$ in the interval $[a,b]$ is a function of Baire class not higher than 2, and \begin{equation}\label{eq1} V_a^b(f) = \int\limits_{-\infty}^{+\infty} N(y, f) \, dy, \end{equation}
where $V_a^b(f)$ is the variation of $f(x)$ on $[a,b]$. Thus, equation \eqref{eq1} can be considered as the definition of the variation of a continuous function $f(x)$. The Banach indicatrix is also defined (preserving equation \eqref{eq1}) for functions with discontinuities of the first kind [3]. The concept of a Banach indicatrix was employed to define the variation of functions in several variables [4], [5].
References
| [1] | S. Banach, "Sur les lignes rectifiables et les surfaces dont l'aire est finie" Fund. Math. , 7 (1925) pp. 225–236 |
| [2] | I.P. Natanson, "Theorie der Funktionen einer reellen Veränderlichen" , H. Deutsch , Frankfurt a.M. (1961) (Translated from Russian) |
| [3] | S.M. Lozinskii, "On the Banach indicatrix" Vestnik Leningrad. Univ. Math. Mekh. Astr. , 7 : 2 pp. 70–87 (In Russian) |
| [4] | A.S. Kronrod, "On functions of two variables" Uspekhi Mat. Nauk , 5 : 1 (1950) pp. 24–134 (In Russian) |
| [5] | A.G. Vitushkin, "On higher-dimensional variations" , Moscow (1955) (In Russian) |
Comments
More generally, for any mapping 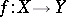 define
define 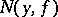 analogously. Then, let
analogously. Then, let 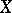 be a separable metric space and let
be a separable metric space and let 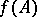 be
be 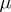 -measurable for all Borel subsets
-measurable for all Borel subsets 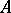 of
of 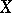 . Let
. Let 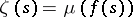 for
for 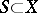 and let
and let 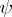 be the measure on
be the measure on 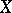 defined by the Carathéodory construction from
defined by the Carathéodory construction from 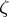 . Then
. Then
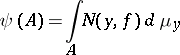 |
for every Borel set 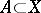 . Cf. [a1], p. 176 ff. For significant extension of (*), cf. [a2].
. Cf. [a1], p. 176 ff. For significant extension of (*), cf. [a2].
References
| [a1] | H. Federer, "Geometric measure theory" , Springer (1969) |
| [a2] | H. Federer, "An analytic characterization of distributions whose partial derivatives are representable by measures" Bull. Amer. Math. Soc. , 60 (1954) pp. 339 |
Banach indicatrix. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Banach_indicatrix&oldid=36410