Balian-Low theorem
A theorem dealing with the representation of arbitrary functions in 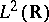 as a sum of time-frequency atoms, or Gabor functions (cf. also Gabor transform), of the form
as a sum of time-frequency atoms, or Gabor functions (cf. also Gabor transform), of the form
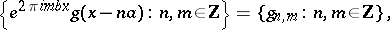 |
where 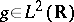 is a fixed window function and
is a fixed window function and 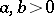 are fixed lattice parameters. The goal is to write an arbitrary function
are fixed lattice parameters. The goal is to write an arbitrary function 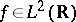 in a series of the form
in a series of the form
 | (a1) |
where the coefficients  depend linearly on
depend linearly on 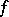 . One requires that the collection
. One requires that the collection 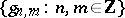 forms a frame for
forms a frame for 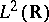 , that is, that there exist constants
, that is, that there exist constants 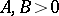 such that for any
such that for any 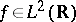 ,
,
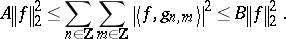 | (a2) |
Inequality (a2) implies the existence of coefficients 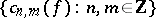 satisfying (a1) and the inequality
satisfying (a1) and the inequality 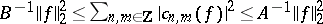 . This inequality can be interpreted as expressing the continuous dependence of
. This inequality can be interpreted as expressing the continuous dependence of 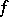 on the coefficients
on the coefficients 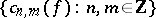 and the continuous dependence of these coefficients on
and the continuous dependence of these coefficients on 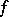 . Whether or not an arbitrary collection of Gabor functions
. Whether or not an arbitrary collection of Gabor functions  forms a frame for
forms a frame for 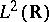 depends on the window function
depends on the window function 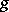 and on the lattice density
and on the lattice density 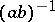 . The lattice density
. The lattice density 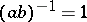 is referred to as the critical density, for the following reason. If
is referred to as the critical density, for the following reason. If 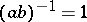 and
and 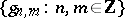 forms a frame, then that frame is non-redundant, i.e., it is a Riesz basis. If
forms a frame, then that frame is non-redundant, i.e., it is a Riesz basis. If 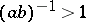 and
and 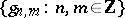 forms a frame, then that frame is redundant, i.e., the representation (a1) is not unique. If
forms a frame, then that frame is redundant, i.e., the representation (a1) is not unique. If 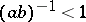 , then for any
, then for any 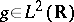 , the collection
, the collection 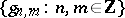 is incomplete. See [a9], [a10].
is incomplete. See [a9], [a10].
The time-frequency atom 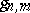 is said to be localized at time
is said to be localized at time 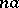 and frequency
and frequency 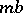 since the Fourier transform of
since the Fourier transform of  is given by
is given by 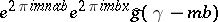 . A window function
. A window function 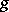 is said to have "good localization" in time and frequency if both
is said to have "good localization" in time and frequency if both 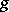 and its Fourier transform
and its Fourier transform 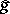 decay rapidly at infinity. Good localization can be measured in various ways. One way is to require that
decay rapidly at infinity. Good localization can be measured in various ways. One way is to require that 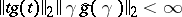 . This is related to the classical uncertainty principle inequality, which asserts that any function
. This is related to the classical uncertainty principle inequality, which asserts that any function 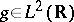 satisfies
satisfies 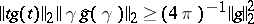 .
.
The Balian–Low theorem asserts that if 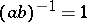 and if
and if 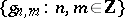 forms a frame for
forms a frame for 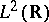 , then
, then 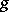 cannot have good localization. Specifically: If
cannot have good localization. Specifically: If  and if
and if 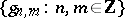 forms a frame for
forms a frame for 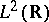 , then
, then 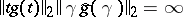 , i.e.,
, i.e., 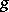 maximizes the uncertainty principle inequality.
maximizes the uncertainty principle inequality.
More generally, the term "Balian–Low theorem" or "Balian–Low-type theorem" can refer to any theorem which asserts time and frequency localization restrictions on the elements of a Riesz basis. Such theorems include, for example, [a4], Thm. 3.2, in which a different criterion for "good localization" for the elements of a Gabor system is used, [a7], Thm. 4.4, in which more general time-frequency lattices for Gabor systems are considered, and [a3], which asserts a time-frequency restriction on bases of wavelets (cf. also Wavelet analysis).
The Balian–Low theorem was originally stated and proved by R. Balian [a1] and independently by F. Low [a8] under the stronger assumption that 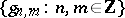 forms an orthonormal basis (cf. also Orthonormal system) for
forms an orthonormal basis (cf. also Orthonormal system) for 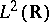 , and an extension of their argument to frames was given by I. Daubechies, R.R. Coifmann and S. Semmes [a5]. An elegant and entirely new proof of the theorem for orthonormal bases using the classical uncertainty principle inequality was given by G. Battle [a2], and an extension of this argument to frames was given by Daubechies and A.J.E.M. Janssen [a6]. Proofs of the Balian–Low theorem for frames use the differentiability properties of the Zak transform in an essential way.
, and an extension of their argument to frames was given by I. Daubechies, R.R. Coifmann and S. Semmes [a5]. An elegant and entirely new proof of the theorem for orthonormal bases using the classical uncertainty principle inequality was given by G. Battle [a2], and an extension of this argument to frames was given by Daubechies and A.J.E.M. Janssen [a6]. Proofs of the Balian–Low theorem for frames use the differentiability properties of the Zak transform in an essential way.
References
| [a1] | R. Balian, "Un principe d'incertitude fort en théorie du signal ou en mécanique quantique" C.R. Acad. Sci. Paris , 292 (1981) pp. 1357–1362 |
| [a2] | G. Battle, "Heisenberg proof of the Balian–Low theorem" Lett. Math. Phys. , 15 (1988) pp. 175–177 |
| [a3] | G. Battle, "Phase space localization theorem for ondelettes" J. Math. Phys. , 30 (1989) pp. 2195–2196 |
| [a4] | J. Benedetto, C. Heil, D. Walnut, "Differentiation and the Balian–Low Theorem" J. Fourier Anal. Appl. , 1 (1995) pp. 355–402 |
| [a5] | I. Daubechies, "The wavelet transform, time-frequency localization and signal analysis" IEEE Trans. Inform. Th. , 39 (1990) pp. 961–1005 |
| [a6] | I. Daubechies, A.J.E.M. Janssen, "Two theorems on lattice expansions" IEEE Trans. Inform. Th. , 39 (1993) pp. 3–6 |
| [a7] | H. Feichtinger, K. Gröchenig, "Gabor frames and time—frequency distributions" J. Funct. Anal. , 146 (1997) pp. 464–495 |
| [a8] | F. Low, "Complete sets of wave packets" C. DeTar (ed.) et al. (ed.) , A Passion for Physics: Essays in Honor of Geoffrey Chew , World Sci. (1985) pp. 17–22 |
| [a9] | M. Rieffel, "Von Neumann algebras associated with pairs of lattices in Lie groups" Math. Ann. , 257 (1981) pp. 403–418 |
| [a10] | J. Ramanathan, T. Steger, "Incompleteness of Sparse Coherent States" Appl. Comput. Harm. Anal. , 2 (1995) pp. 148–153 |
Balian-Low theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Balian-Low_theorem&oldid=17611