Baire theorem
Baire's theorem on complete spaces: Any countable system of open and everywhere-dense sets in a given complete metric space has a non-empty, and even an everywhere-dense, intersection in this space. An equivalent formulation is the following: A non-empty complete metric space cannot be represented as a countable sum of its nowhere-dense subsets. Stated by R. Baire [1].
References
| [1] | R. Baire, Ann. Mat. Pura Appl. , 3 (1899) pp. 67 |
Comments
This theorem is also known as the Baire category theorem (cf. [a1], p. 200).
References
| [a1] | J.L. Kelley, "General topology" , v. Nostrand (1955) |
Baire's theorem on semi-continuous functions: Let 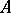 be a subset of a metric space
be a subset of a metric space 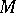 , and let
, and let 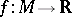 . The condition: For any number
. The condition: For any number  the set
the set 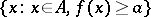 (or, respectively,
(or, respectively, 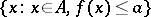 ) is closed in
) is closed in 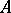 , is necessary and sufficient for
, is necessary and sufficient for 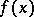 to be semi-continuous from above (or, respectively, from below) on
to be semi-continuous from above (or, respectively, from below) on 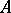 . Demonstrated by R. Baire for
. Demonstrated by R. Baire for 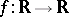 [1]. It follows from this theorem that semi-continuous functions belong to the first Baire class (cf. Baire classes). A stronger theorem is valid: A function that is semi-continuous from above (from below) and that does not assume the value
[1]. It follows from this theorem that semi-continuous functions belong to the first Baire class (cf. Baire classes). A stronger theorem is valid: A function that is semi-continuous from above (from below) and that does not assume the value 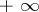 (
(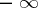 ) is the limit of a monotone non-increasing (non-decreasing) sequence of continuous functions.
) is the limit of a monotone non-increasing (non-decreasing) sequence of continuous functions.
References
| [1] | R. Baire, "Leçons sur les fonctions discontinues, professées au collège de France" , Gauthier-Villars (1905) |
| [2] | I.P. Natanson, "Theorie der Funktionen einer reellen Veränderlichen" , H. Deutsch , Frankfurt a.M. (1961) (Translated from Russian) |
I.A. Vinogradova
Comments
A function in the first Baire class is also called a Baire function.
References
| [a1] | W. Rudin, "Principles of mathematical analysis" , McGraw-Hill (1964) |
Baire theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Baire_theorem&oldid=13173