Baire property
of a set 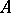 in a topological space
in a topological space
A property analogous to the measurability of a set. A set 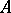 has the Baire property if there exists an open set
has the Baire property if there exists an open set 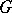 such that the differences
such that the differences 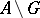 and
and  are sets of the first category according to Baire (cf. Category of a set); the term "open" may be replaced by "closed" . There are other equivalent definitions; thus, for instance, a set has the Baire property if it is the union of a set of type
are sets of the first category according to Baire (cf. Category of a set); the term "open" may be replaced by "closed" . There are other equivalent definitions; thus, for instance, a set has the Baire property if it is the union of a set of type 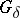 and a set of the first category. The class of sets with the Baire property is closed under the operations of complementing, taking countable unions and taking countable intersections. For an example of a set which does not have the Baire property, see [1].
and a set of the first category. The class of sets with the Baire property is closed under the operations of complementing, taking countable unions and taking countable intersections. For an example of a set which does not have the Baire property, see [1].
Comments
A set with the Baire property is often called a Baire set or an almost-open set. A set of the first category is often called meager.
References
| [Ba] | R. Baire, "Leçons sur les fonctions discontinues, professées au collège de France" , Gauthier-Villars (1905) Zbl 36.0438.01 |
| [Ku] | K. Kuratowski, "Topology" , 1–2 , Acad. Press (1966–1968) MR0259835 MR0217751 Zbl 0158.40802 |
| [Ox] | J.C. Oxtoby, "Measure and category" , Springer (1971) MR0393403 0217.09201 Zbl 0217.09201 |
| [Ro] | H.L. Royden, "Real analysis", Macmillan (1968) MR0151555 Zbl 0197.03501 |
| [a1] | E. Čech, "Topological spaces" , Wiley (1966) MR0211373 Zbl 0141.39401 |
Baire property. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Baire_property&oldid=28326