Baire property
of a set 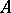 in a topological space
in a topological space
A property analogous to the measurability of a set. A set 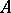 has the Baire property if there exists an open set
has the Baire property if there exists an open set 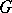 such that the differences
such that the differences 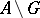 and
and  are sets of the first category according to Baire (cf. Category of a set); the term "open" may be replaced by "closed" . There are other equivalent definitions; thus, for instance, a set has the Baire property if it is the union of a set of type
are sets of the first category according to Baire (cf. Category of a set); the term "open" may be replaced by "closed" . There are other equivalent definitions; thus, for instance, a set has the Baire property if it is the union of a set of type 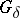 and a set of the first category. The class of sets with the Baire property is closed under the operations of complementing, taking countable unions and taking countable intersections. For an example of a set which does not have the Baire property, see [1].
and a set of the first category. The class of sets with the Baire property is closed under the operations of complementing, taking countable unions and taking countable intersections. For an example of a set which does not have the Baire property, see [1].
Comments
A set with the Baire property is often called a Baire set or an almost-open set. A set of the first category is often called meager.
References
| [Ba] | R. Baire, "Leçons sur les fonctions discontinues, professées au collège de France" , Gauthier-Villars (1905) Zbl 36.0438.01 |
| [Ku] | K. Kuratowski, "Topology" , 1–2 , Acad. Press (1966–1968) MR0345085 MR0339039 MR0346724 MR0259836 MR0259835 MR0234404 MR0217751 MR0217750 MR1532625 MR0161299 MR0155280 MR0175070 Zbl 0849.01044 Zbl 0528.54033 Zbl 1081.54501 Zbl 0383.54001 Zbl 0323.54010 Zbl 0274.54007 Zbl 0267.54002 Zbl 0247.54001 Zbl 0163.17002 Zbl 0158.40901 Zbl 0158.40802 Zbl 0148.42801 Zbl 0104.27402 Zbl 0098.24110 Zbl 0137.15604 Zbl 0041.09604 Zbl 0041.09603 Zbl 0008.13202 Zbl 56.0517.04 |
| [Ox] | J.C. Oxtoby, "Measure and category" , Springer (1971) MR0393403 0217.09201 Zbl 0217.09201 |
| [Ro] | H.L. Royden, "Real analysis", Macmillan (1968) MR0151555 Zbl 0197.03501 |
| [a1] | E. Čech, "Topological spaces" , Wiley (1966) MR0211373 Zbl 0141.39401 |
Baire property. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Baire_property&oldid=28322