Baire property

of a set 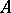in a topological space

A property analogous to the measurability of a set. A set 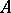has the Baire property if there exists an open set 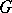such that the differences 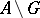and are sets of the first category according to Baire (cf. Category of a set); the term "open" may be replaced by "closed" . There are other equivalent definitions; thus, for instance, a set has the Baire property if it is the union of a set of type 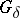and a set of the first category. The class of sets with the Baire property is closed under the operations of complementing, taking countable unions and taking countable intersections. For an example of a set which does not have the Baire property, see [1].

References

[1]	K. Kuratowski, "Topology" , 1–2 , Acad. Press (1966–1968) (Translated from French) (Paragraph 40)

Comments

A set with the Baire property is often called a Baire set or an almost-open set. A set of the first category is often called meager.

References

[a1]	E. Čech, "Topological spaces" , Wiley (1966)